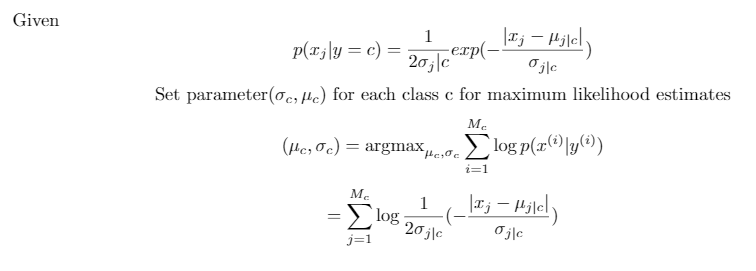
Exercise 2 [5 points]. Given a training set D = {(x(), y(?) ), i = 1, ..., M}, where a() E RN and y(?) c {1, 2, ..., C}, derive the maximum likelihood estimates of the naive Bayes for real valued ," modeled with a Laplacian distribution, i.e., p(x; ly = c) = 1 20 jlc exp Ojc Exercise 3 [5 points]. Prove that in binary classification, the posterior of linear discrim inant analysis, i.e., p(y = 1/x; 4, /, >), is in the form of a sigmoid function p(y = 1x; 0) = 1 +e-07 x' (1) where O is a function of {y, , E}. Hint: remember to use the convention of letting To = 1 that incorporates the bias term into the parameter vector 0.Given p(cj ly = c) = exp(- Oilc Set parameter(c, #c) for each class c for maximum likelihood estimates Mc (He, c) = argmax, log p(x() ly(2)) i=1 Mc = E 1 log Ij - Pylel j=1 20jc Ojc