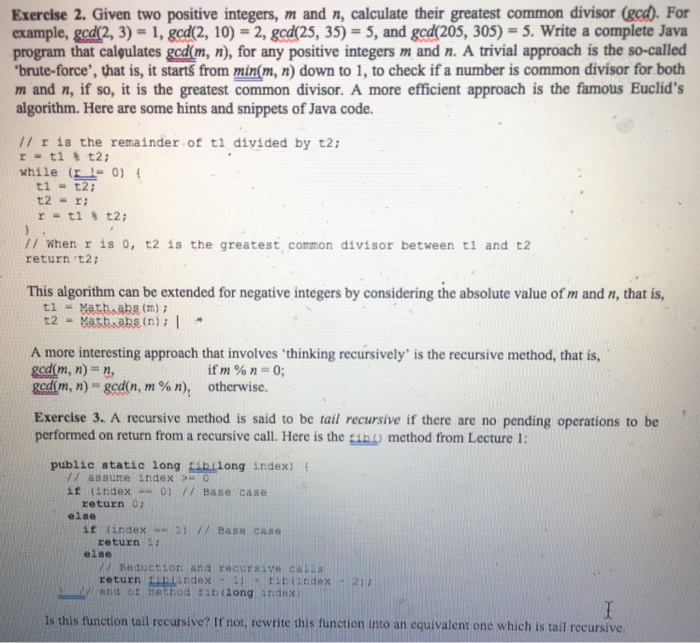
Exercise 2. Given two positive integers, m and n, calculate their greatest common divisor (gcd). For example, god2, 3)-1,gcd(2, 10) -2, gcd25, 35)-5, and gcd(205, 305) -5. Write a complete Java program that calgulates gcd(m, n), for any positive integers m and n. A trivial approach is the so-called brute-force', that is, it start from min(m, n) down to 1, to check if a number is common divisor for both m and n, if so, it is the greatest common divisor. A more efficient approach is the famous Euclid's algorithm. Here are some hints and snippets of Java code. lI r is the remainder of ti divided by t2: while ( 0) tl-t2 t2 ri // When r is 0, t2 is the greatest, common divisor between t1 and t2 return t2; This algorithm can be extended for negative integers by considering the absolute value of m and n, that is, ti -atb.abs (m) A more interesting approach that involves thinking recursively' is the recursive method, that is, gcd(m, n)- n get(m, n) = gcd(n, m % n), otherwise ifm % n = 0; Exercise 3. A recursive method is said to be tail recursive if there are no pending operations to be performed on return from a recursive call. Here is the tih method from Lecture 1: public static long tibilong index) t assume index 0 return 0 it (index // Base, case if (index-0 // Base.case else return t else // Reductiion and recursive caius return aAndex 1AD(ndex 21 end ot method Fib (long indnx is this function tail recursive? If not, rewrite this function into an equivalent one which is tail recursive