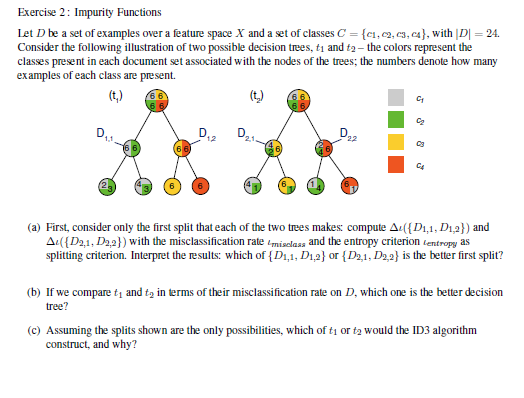
Exercise 2: Impurity Functions Let D be a set of examples over a feature space X and a set of classes C = {1,2,43,c}, with |D = 24. Consider the following illustration of two possible decision trees, ti and t2 - the colors represent the classes present in each document set associated with the nodes of the trees, the numbers denote how many examples of each class are present. (t) (ty) D D21 D2 C4 (a) First, consider only the first split that each of the two trees makes compute A:({D1,1, D1,2)) and A1({D2,1, D2,2}) with the misclassification rate misclass and the entropy criterion lentropy as splitting criterion. Interpret the results: which of {D1,1, D1,2} or {D2,1, D2.2} is the better first split? (b) If we compare tand tz in terms of their misclassification rate on D, which one is the better decision tree? (C) Assuming the splits shown are the only possibilities, which of t1 or ty would the ID3 algorithm construct, and why