Question: Exercise 2.5.9: a) Prove that if EX, and Eyn converge absolutely, then EXnyn converges absolutely. b) Find an explicit example where the converse does not

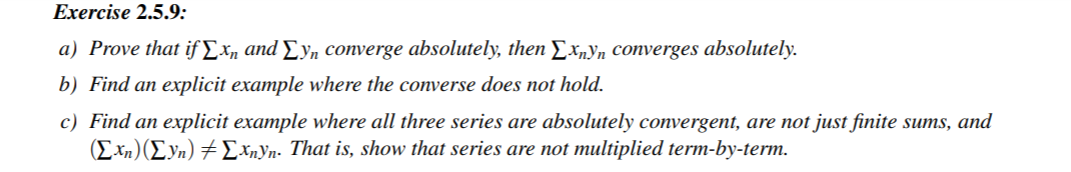
Exercise 2.5.9: a) Prove that if EX, and Eyn converge absolutely, then EXnyn converges absolutely. b) Find an explicit example where the converse does not hold. c) Find an explicit example where all three series are absolutely convergent, are not just finite sums, and (Exn) (Eyn) # [xnyn. That is, show that series are not multiplied term-by-term

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Could you please help with question 263 and 264? Thanks 5.3 Difference Equations So what can we do with spectral decompositions that we could not do with the SVD? We have already seen examples, like...

Could you please help with question 261 and 262? Thanks 5.3 Difference Equations So what can we do with spectral decompositions that we could not do with the SVD? We have already seen examples, like...

M Question 5 - Capacity Decision X C Suresh Company reports the fo X + C...

Show that a matrix is: i) Hermitian if and only if it can be diagonalized using an orthonormal basis of eigenvectors and the eigenvalues are real; ii) skew Hermitian if and only if it can be...

With reference to the lumber-strength data in Exercise 2.59, the statistical software package $S A S$ produced the output in Figure 2.20. Using this output, (a) identify the mean and standard...

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

2.74 With reference to the lumber-strength data in Exercise 2.59, the statistical software package SAS produced the output in Figure 2.20. Using this output, (a) identify the mean and standard...

Kindly answer part 1 and part 2. Upvote guaranteed Exercise 25-9 Part 2 (2) Management eliminates departments with sales dollars that are less than avoidable expenses. DEPARTMENTS WITH LESS SALES...

thx love ya Check my Required information Exercise 25-9 Analyzing income effects from eliminating departments LO P4 [The following information applies to the questions displayed below) Suresh Co....

What is meant by time value of money and how it is applicable for organizations to consider the effects?

The IBM System/370 architecture uses a two-level memory structure and refers to the two levels as segments and pages, although the segmentation approach lacks many of the features described earlier...

which of the following statements regarding contributions to defined contribution plans is false? a . employers bear investment risks

2023 1040 form 1.Phillip and Claire are married and file a joint return. Phillip is self-employed as a real estate agent, and Claire is a flight attendant. Phillip and Claire have three dependent...