Exercise 3\ Consider the function

f:[0,\\\\infty )->R

given by

f(x)=x^(2)+xcos(x)

for all

x>=0

.\ Gegeven is de functie

f:[0,\\\\infty )->R

met

f(x)=x^(2)+xcos(x)

voor alle

x>=0

.\ 3a Show that the function

f

is one-to-one.\ Bewijs dat de functie

f

injectief is.

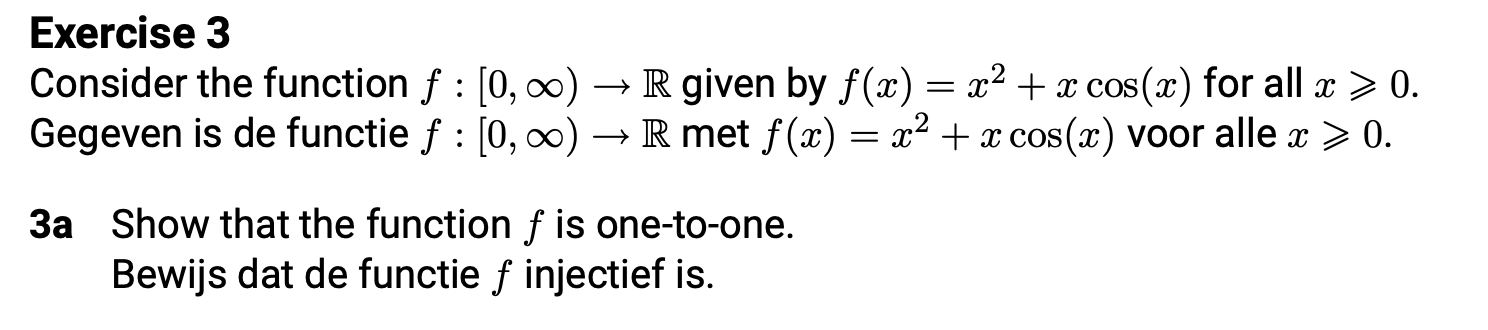
Consider the function f:[0,)R given by f(x)=x2+xcos(x) for all x0. Gegeven is de functie f:[0,)R met f(x)=x2+xcos(x) voor alle x0. 3a Show that the function f is one-to-one. Bewijs dat de functie f injectief is