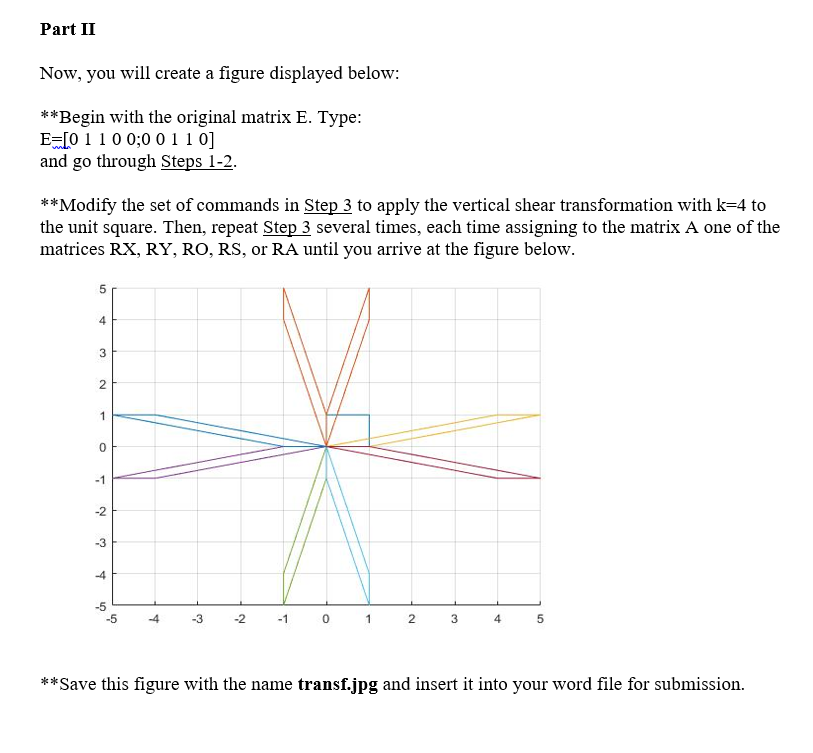
Exercise 6 (4 points) Difficulty: Moderate In this exercise, you will plot figures in xy -plane and consider their images under the transformations of the plane such as reflections and shears **First, create two functions in MATLAB: function vs - vrsh (k) and function HS-hrsh (k) that will generate the standard matrices for the vertical and horizontal shears, respectively, defined by a parameter k. (For help, see Module 9 lecture and read Section 1.9 of the textbook.) **Type the functions rsh and hrsh in your diary file. **Store on your workspace (and in your diary file) the standard matrices, which names are listed below, for the transformation indicated in the parentheses: RX (reflection across the x-axis) RY(reflection across the y-axis) RQ(rotation through 180 degrees around the Origin) RS (reflection across the line y = x ) RA (reflection across the line y =-x) For example, to store RX, type on the workspace (and save it in the diary file): RX LI 0; 0-1] and hit "Enter". Do not suppress the output (no semicolon at the end **Next, create the following function in the file in MATLAB, which takes as inputs a 2 x 5 matrix E and a 2 x 2 matrix A. The input E is a matrix whose columns are the coordinate vectors of the vertices of a closed polygonal line, and a matrix A will be one of the standard matrices created above (VS, HS, RX, RX, RY, RO, RS, or RA) Exercise 6 (4 points) Difficulty: Moderate In this exercise, you will plot figures in xy -plane and consider their images under the transformations of the plane such as reflections and shears **First, create two functions in MATLAB: function vs - vrsh (k) and function HS-hrsh (k) that will generate the standard matrices for the vertical and horizontal shears, respectively, defined by a parameter k. (For help, see Module 9 lecture and read Section 1.9 of the textbook.) **Type the functions rsh and hrsh in your diary file. **Store on your workspace (and in your diary file) the standard matrices, which names are listed below, for the transformation indicated in the parentheses: RX (reflection across the x-axis) RY(reflection across the y-axis) RQ(rotation through 180 degrees around the Origin) RS (reflection across the line y = x ) RA (reflection across the line y =-x) For example, to store RX, type on the workspace (and save it in the diary file): RX LI 0; 0-1] and hit "Enter". Do not suppress the output (no semicolon at the end **Next, create the following function in the file in MATLAB, which takes as inputs a 2 x 5 matrix E and a 2 x 2 matrix A. The input E is a matrix whose columns are the coordinate vectors of the vertices of a closed polygonal line, and a matrix A will be one of the standard matrices created above (VS, HS, RX, RX, RY, RO, RS, or RA)