Question: Exercise 6.1. Prove identity (6.5). Hint. Make the necessary changes in the proof of Theorem 2.12.Pu(Xo = y) = u(y) and Pr(Xo = x) =

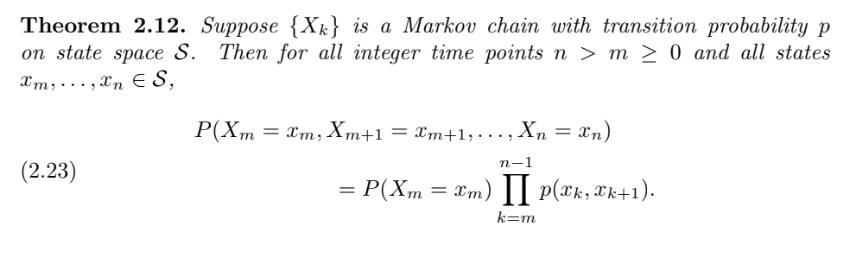
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


