Exercise Problem

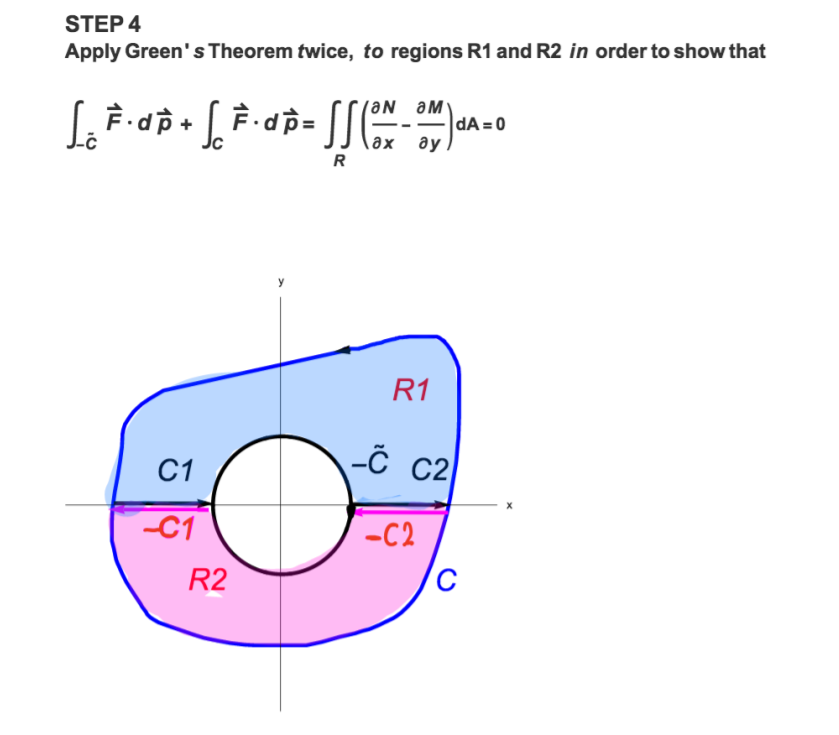
STEP 2 ON aM Show that -=0. ax ay Is the vector field F coservative (gradient) ? Explain! STEP 3 Explain why we cannot apply the Green's Theorem to the region R, i.e., we cannot claim that the following is true by the Green's Theorem : F . dp + J F. ap = JJ(ox -on ) da=0 R\fSTEP 4 Apply Green's Theorem twice, to regions R1 and R2 in order to show that [. F . dp + [ F. ap= JJ(ox -on ) dA=0 R R1 C1 -C C2 C1 -C2 R2 CConsider the vector field : F (x, y) = (M (x, y), N(x, y)> = 2 + y?' x2 + y Let C be any simple, positively oriented, closed curve that encloses the origin. Show that : SF . dp=2x. We will solve this problem by completing the following steps : STEP 1 Let C be a positively oriented circle of radius r with the center at the origin. Let r be so small that the circle C lies within the region enclosed by the curve C (see figure below). Compute the integral S. F . ap. R C C