Explain and solve this example

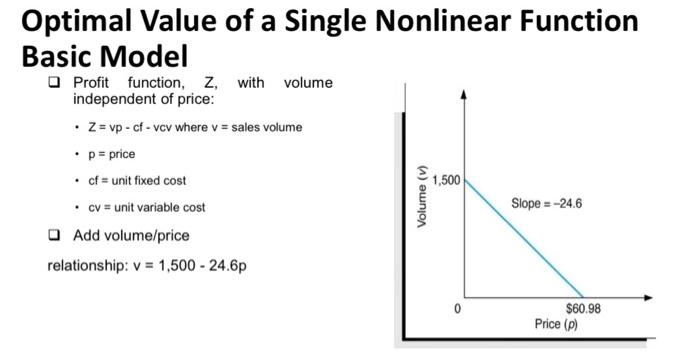
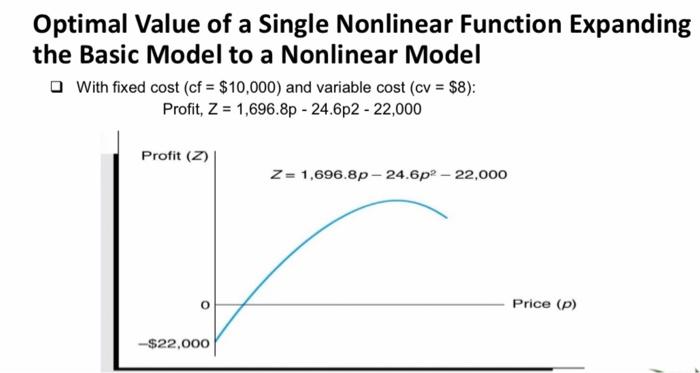
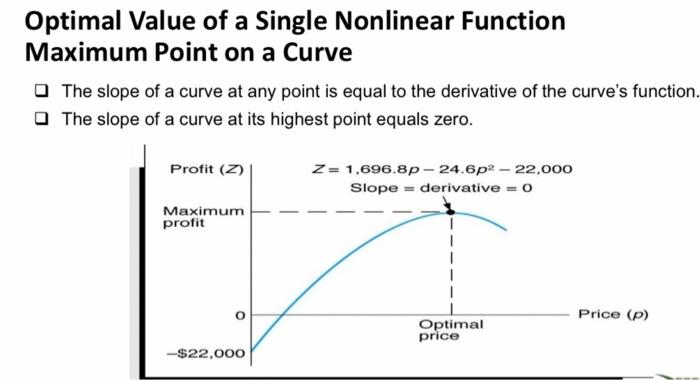
Optimal Value of a Single Nonlinear Function Basic Model Profit function, Z, with volume independent of price: - Z=vp - cf - vcv where v= sales volume - p= price - cf= unit fixed cost - cv= unit variable cost Add volume/price relationship: v=1,50024.6p Optimal Value of a Single Nonlinear Function Expanding the Basic Model to a Nonlinear Model With fixed cost (cf=$10,000) and variable cost (cv=$8) : Profit, Z=1,696.8p24.6p222,000 Optimal Value of a Single Nonlinear Function Maximum Point on a Curve The slope of a curve at any point is equal to the derivative of the curve's function The slope of a curve at its highest point equals zero