explain what the problem is and what Excel is doing

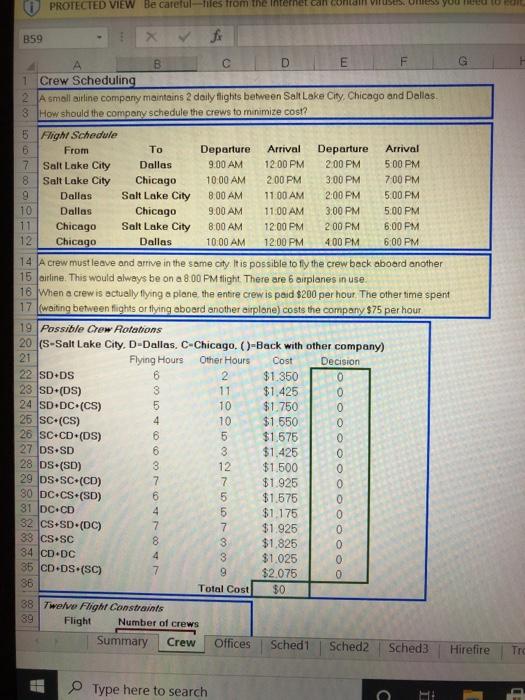
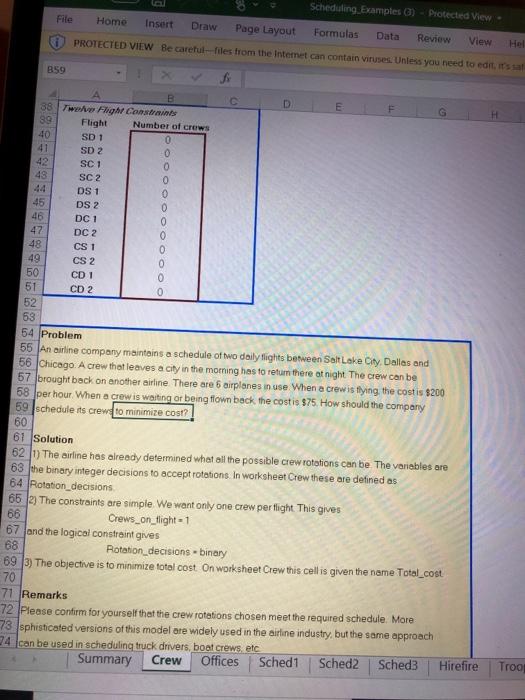
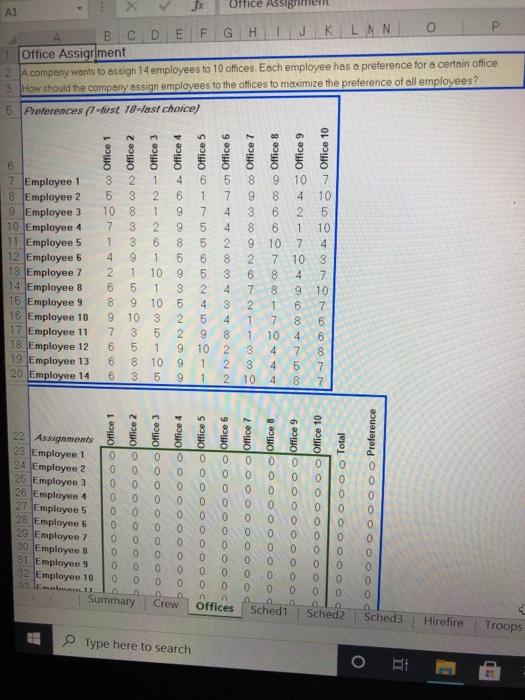
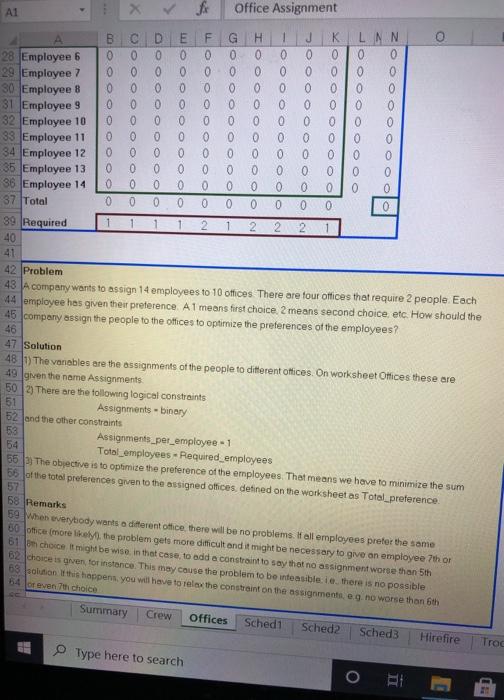
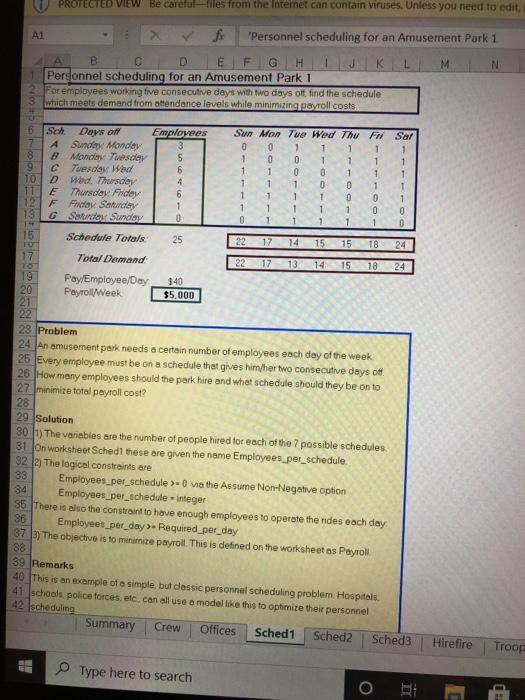
PROTECTED VIEW Be carefullies from the Internet can contain Viruses. Unless you B59 B D E 1 Crew Scheduling 2 A small airline company maintains 2 daily flights between Salt Lake City, Chicago and Dallas 3. How should the company schedule the crews to minimize cost? 5 Fight Schedule 6 From To Departure Arrival Departure Arrival 7 Salt Lake City Dallas 9.00 AM 12:00 PM 2.00 PM 5:00 PM 8 Salt Lake City Chicago 10.00 AM 2.00 PM 3.00 PM 7:00 PM 9 Dallas Salt Lake City 8.00 AM 11:00 AM 2:00 PM 5:00 PM 10 Dallas Chicago 9.00 AM 11:00 AM 3,00 PM 5:00 PM 11 Chicago Salt Lake City 8:00 AM 12:00 PM 2 00 PM 6:00 PM 12 Chicago Dallas 10.00 AM 12:00 PM 4:00 PM 600 PM 14 A crew must leave and arrive in the same city. It is possible to fly the crew back aboard another 15 airline. This would always be on a 8 00 PM Hlight. There are 6 airplanes in use. 16 When a crew is actually flying a plane the entire crew is paid $200 per hour The other time spent 17 waiting between flights or flying aboard another airplane) costs the company $75 per hour 19 Possible Crow Rotations 20 (S-Salt Lake City, D-Dallas, C-Chicago. ()-Back with other company) 21 Flying Hours Other Hours Cost Decision 22 SD DS 6 2 $1.350 0 23 SD (DS) 3 11 $1.425 24 SD.DC (CS) 5 10 $1.750 26 SC (CS) 4 10 $1.550 26 SC+CD+CDS) 6 5 $1.575 27 DS.SD 6 3 $1,425 28 DS (SD) 3 12 $1.500 29 DS.SC (CD) 7 7 $1.925 80 DC.CS (SD) 6 5 $1.575 31 DC.CD 4 5 $1.175 32 CS SD-(DC) 7 7 $1.925 33 CS SC 8 $1,826 34 CD DC 4 3 $1.025 35 CD.DS (SC) 7 $2.075 86 Total Cost $0 38 Twelve Flight Constraints 89 Flight Number of crews Summary Crew Offices Sched1 Sched2 Sched3 Hirefire 0 0 0 0 OOOOOOOO Tre Type here to search C Scheduling Examples (3) Protected View - File Home Insert Draw Page Layout Formulas Data PROTECTED VIEW Be careful--files from the Internet can contain viruses. Unless you need to edit it's al Review View Hol B59 DS 2 OOOOOOOOO B D E H 88 Two Flight Contri 39 Flight Number of crews 40 SD 1 0 41 SD 2 0 42 SC 1 49 SC 2 DS 1 45 46 DC 1 47 DC 2 48 CS1 49 CS 2 50 CD 1 51 CD 2 0 52 63 54 Problem 55 An airline company maintains a schedule of two daily lights between Salt Lake City, Dallas and 56 Chicago. A crew that leaves a city in the morning has to return there at night. The crew can be 57 brought back on another airline There are 6 airplanes in use When a crewis tlying the cost is $200 58 per hour When a crew is waiting or being flown back the costis $75. How should the company 59 schedule its crew to minimize cost? 60 61 Solution 62 (1) The airline has already determined what all the possible crew rotations can be The variables are 63 the binary integer decisions to accept rotations in worksheet Crew these are defined as 64 Rotation_decisions 652) The constraints are simple. We want only one crew per flight This gives 66 Crews_on_light = 1 67 and the logical constraint gives 68 Rotation decisions - binary 693) The objective is to minimize total cost On worksheet Crew this cellis given the name Total_cost 70 71 Remarks 72 Please confirm for yourself that the crew rotations chosen meet the required schedule. More 73 sphisticated versions of this model are widely used in the airline industry, but the same approach 34 can be used in scheduling truck drivers, boat crews etc Summary Crew Offices Sched1 Sched2 Sched Hirefire Troo Office Assi A1 1 D E F G HJ K L M N O Office Assigriment 2 A company wants to assign 14 employees to 10 offices. Each employee has a preference for a certain office 3 How should the company assign employees to the offices to maximize the preference of all employees? 5. Preferences (1-first 10-last choice) 9 CO NAJoco Office 1 7 Employee 1 8 Employee 2 9 Employee 3 10 Employee 4 11 Employee 5 12 Employee 6 13 Employee 7 14 Employee 8 15 Employee 9 16 Employee 10 17 Employee 11 18 Employee 12 19 Employee 13 20 Employee 14 1 7 5 5 ONN OG TOOOO Office 4 2 1 3 2 10 8 1 3 2 3 6 9 1 1 10 6 5 1 8 9 10 9 103 7 3 5 6 5 1 6 8 10 6 3 5 - OAN - Office 5 9 5 8 7 9 4 3 4 2 8 2 6 4 7 2 4 1 8 1 2 3 2 3 2 10 AO-0000OOOOO Office 8 9 10 8 4 6 2 6 1 10 7 10 8 4 8 9 1 6 7 8 4 7 4 5 4 8 000001 Office 10 0 0 0 A-NAOffice 9 9 8 7 7 6 1 0 OO JOffice 2 0 0 0 0 0 0 0 0 22 Assignments 28 Employee 1 24 Employee 2 25 Employee 3 26 Employee 4 27 Employee 5 28 Employees 29 Employee 7 90 Employee S1 Employees 32 Employee 10 Summary OOOOOOOOO JOffice 1 BOOOOOOOO O Office 3 POOOOOOOOO JOffice 4 0 OOOOOOOOOO JOffice 5 OOOOOOOOO JOffice 6 BOOOOOOOOO JOffice 7 OOOOOOOOO JOffice 8 OOOOOOOOO JOffice 9 OOOOOOOOO JOffice 10 OOOOOOOOOO Preference OOOOOOOO Total 0 Crew Offices Schedi Sched2 Sched3 Hirefire Troops 3 Type here to search A1 Office Assignment E F 1 0 0 0 K 0 0 LNN 0 0 0 0 BOOOOOOOOO 28 Employee 6 29 Employee 7 30 Employee 8 31 Employee 9 32 Employee 10 33 Employee 11 34 Employee 12 35 Employee 13 86 Employee 14 37 Total 39 Required 40 OOOOOOOOOO GOOOOOOOOOO - olooOOOOOOO OOOOOOOOOO GOOOOOOOOOO 0 0 O O O O O O 0 0 0 0 OOOO 0 0 0 0 0 0 0 0 0 1 1 2 1 2 2 2 42 Problem 43 A company wants to assign 14 employees to 10 offices. There are four offices that require 2 people. Each 44 employee has given their preference. A1 means first choice 2 means second choice, etc. How should the 45 company assign the people to the offices to optimize the preferences of the employees? 46 47 Solution 48 1) The vonables are the assignments of the people to different offices. On worksheet Offices these are 49 given the name Assignments 50 2) There are the following logical constraints 51 Assignments - binary 52 and the other constraints 53 Assignments_per_employee - 1 54 Total_employees. Required_employees 55) The objective is to optimize the preference of the employees. That means we have to minimize the sum 56 of the total preferences given to the assigned offices, defined on the worksheet as Total_preference 57 58 Remarks 59 When everybody wants a different office there will be no problems. If all employees prefer the same 80 office (more likely. The problem gets more difficult and it might be necessary to give an employee 7th or 61 on choice it might be wise in that case to add a constraint to say that no assignment worse than 5th 62 choice is given for instance. This may cause the problem to be inteasible ie, there is no possible 63 solution this topper, you will have to relax the constraint on the assignments, eg no worse than 6th 54 or even 7th choice Summary Crew Offices Sched Sched2 Sched Hire fire Troc Type here to search o BE PROTECTED VIEW Be Careful--files from the Internet can contain viruses. Unless you need to edit 1 'Personnel scheduling for an Amusement Park 1 B C D E F G H 1 K L M N Personnel scheduling for an Amusement Park 1 For employees working five consecutive days with two days off, find the schedule 3 which meets demand from attendance levels while minimizing payroll costs 6 Sch Days off Employees A anaiMemory 3 8 B Monday Tuesday 5 9 Cinesday Wed 6 10 D Wed Thursday 4 TE Thursday Friday 6 12 F Friday Saturday 1 13 G Saturday Sunday 0 15 Schedule Totals 25 Sun Mon Tue Wed Thu Fri Sal 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 O 0 0 1 1 1 1 1 0 22 17 14 15 15 18 24 17 Total Demand 22 17 13 14 15 18 24 19 Pay/Employee/Day $40 20 Payroll/Week $5,000 21 22 23 Problem 24 An amusement park needs a certain number of employees each day of the week 25 Every employee must be on a schedule that gives him/her two consecutive days of 26 How many employees should the park hire and what schedule should they be on to 27 minimize total payroll cost? 28 29 Solution 301) The variables are the number of people hired for each of the 7 possible schedules 31 on worksheet Sched these are given the name Employees_per_schedule 32 2) The logical constraints are 83 Employees_per_schedule >=0 via the Assume Non-Negative option 34 Employees_per_schedule - integer 35 There is also the constraint to have enough employees to operate the rides each day 36 Employees_per_day>- Required_per_day 875) The objective is to minimize payroll. This is defined on the worksheet os Payroll 88 39 Remarks 40 This is an example of a simple but classic personnel scheduling problem Hospitals 41 schools, police forces, etc. can all use a model like this to optimize their personnel Summary Crew Offices Sched1 Sched2 Sched3 42 scheduling Hirefire Troop Type here to search PROTECTED VIEW Be carefullies from the Internet can contain Viruses. Unless you B59 B D E 1 Crew Scheduling 2 A small airline company maintains 2 daily flights between Salt Lake City, Chicago and Dallas 3. How should the company schedule the crews to minimize cost? 5 Fight Schedule 6 From To Departure Arrival Departure Arrival 7 Salt Lake City Dallas 9.00 AM 12:00 PM 2.00 PM 5:00 PM 8 Salt Lake City Chicago 10.00 AM 2.00 PM 3.00 PM 7:00 PM 9 Dallas Salt Lake City 8.00 AM 11:00 AM 2:00 PM 5:00 PM 10 Dallas Chicago 9.00 AM 11:00 AM 3,00 PM 5:00 PM 11 Chicago Salt Lake City 8:00 AM 12:00 PM 2 00 PM 6:00 PM 12 Chicago Dallas 10.00 AM 12:00 PM 4:00 PM 600 PM 14 A crew must leave and arrive in the same city. It is possible to fly the crew back aboard another 15 airline. This would always be on a 8 00 PM Hlight. There are 6 airplanes in use. 16 When a crew is actually flying a plane the entire crew is paid $200 per hour The other time spent 17 waiting between flights or flying aboard another airplane) costs the company $75 per hour 19 Possible Crow Rotations 20 (S-Salt Lake City, D-Dallas, C-Chicago. ()-Back with other company) 21 Flying Hours Other Hours Cost Decision 22 SD DS 6 2 $1.350 0 23 SD (DS) 3 11 $1.425 24 SD.DC (CS) 5 10 $1.750 26 SC (CS) 4 10 $1.550 26 SC+CD+CDS) 6 5 $1.575 27 DS.SD 6 3 $1,425 28 DS (SD) 3 12 $1.500 29 DS.SC (CD) 7 7 $1.925 80 DC.CS (SD) 6 5 $1.575 31 DC.CD 4 5 $1.175 32 CS SD-(DC) 7 7 $1.925 33 CS SC 8 $1,826 34 CD DC 4 3 $1.025 35 CD.DS (SC) 7 $2.075 86 Total Cost $0 38 Twelve Flight Constraints 89 Flight Number of crews Summary Crew Offices Sched1 Sched2 Sched3 Hirefire 0 0 0 0 OOOOOOOO Tre Type here to search C Scheduling Examples (3) Protected View - File Home Insert Draw Page Layout Formulas Data PROTECTED VIEW Be careful--files from the Internet can contain viruses. Unless you need to edit it's al Review View Hol B59 DS 2 OOOOOOOOO B D E H 88 Two Flight Contri 39 Flight Number of crews 40 SD 1 0 41 SD 2 0 42 SC 1 49 SC 2 DS 1 45 46 DC 1 47 DC 2 48 CS1 49 CS 2 50 CD 1 51 CD 2 0 52 63 54 Problem 55 An airline company maintains a schedule of two daily lights between Salt Lake City, Dallas and 56 Chicago. A crew that leaves a city in the morning has to return there at night. The crew can be 57 brought back on another airline There are 6 airplanes in use When a crewis tlying the cost is $200 58 per hour When a crew is waiting or being flown back the costis $75. How should the company 59 schedule its crew to minimize cost? 60 61 Solution 62 (1) The airline has already determined what all the possible crew rotations can be The variables are 63 the binary integer decisions to accept rotations in worksheet Crew these are defined as 64 Rotation_decisions 652) The constraints are simple. We want only one crew per flight This gives 66 Crews_on_light = 1 67 and the logical constraint gives 68 Rotation decisions - binary 693) The objective is to minimize total cost On worksheet Crew this cellis given the name Total_cost 70 71 Remarks 72 Please confirm for yourself that the crew rotations chosen meet the required schedule. More 73 sphisticated versions of this model are widely used in the airline industry, but the same approach 34 can be used in scheduling truck drivers, boat crews etc Summary Crew Offices Sched1 Sched2 Sched Hirefire Troo Office Assi A1 1 D E F G HJ K L M N O Office Assigriment 2 A company wants to assign 14 employees to 10 offices. Each employee has a preference for a certain office 3 How should the company assign employees to the offices to maximize the preference of all employees? 5. Preferences (1-first 10-last choice) 9 CO NAJoco Office 1 7 Employee 1 8 Employee 2 9 Employee 3 10 Employee 4 11 Employee 5 12 Employee 6 13 Employee 7 14 Employee 8 15 Employee 9 16 Employee 10 17 Employee 11 18 Employee 12 19 Employee 13 20 Employee 14 1 7 5 5 ONN OG TOOOO Office 4 2 1 3 2 10 8 1 3 2 3 6 9 1 1 10 6 5 1 8 9 10 9 103 7 3 5 6 5 1 6 8 10 6 3 5 - OAN - Office 5 9 5 8 7 9 4 3 4 2 8 2 6 4 7 2 4 1 8 1 2 3 2 3 2 10 AO-0000OOOOO Office 8 9 10 8 4 6 2 6 1 10 7 10 8 4 8 9 1 6 7 8 4 7 4 5 4 8 000001 Office 10 0 0 0 A-NAOffice 9 9 8 7 7 6 1 0 OO JOffice 2 0 0 0 0 0 0 0 0 22 Assignments 28 Employee 1 24 Employee 2 25 Employee 3 26 Employee 4 27 Employee 5 28 Employees 29 Employee 7 90 Employee S1 Employees 32 Employee 10 Summary OOOOOOOOO JOffice 1 BOOOOOOOO O Office 3 POOOOOOOOO JOffice 4 0 OOOOOOOOOO JOffice 5 OOOOOOOOO JOffice 6 BOOOOOOOOO JOffice 7 OOOOOOOOO JOffice 8 OOOOOOOOO JOffice 9 OOOOOOOOO JOffice 10 OOOOOOOOOO Preference OOOOOOOO Total 0 Crew Offices Schedi Sched2 Sched3 Hirefire Troops 3 Type here to search A1 Office Assignment E F 1 0 0 0 K 0 0 LNN 0 0 0 0 BOOOOOOOOO 28 Employee 6 29 Employee 7 30 Employee 8 31 Employee 9 32 Employee 10 33 Employee 11 34 Employee 12 35 Employee 13 86 Employee 14 37 Total 39 Required 40 OOOOOOOOOO GOOOOOOOOOO - olooOOOOOOO OOOOOOOOOO GOOOOOOOOOO 0 0 O O O O O O 0 0 0 0 OOOO 0 0 0 0 0 0 0 0 0 1 1 2 1 2 2 2 42 Problem 43 A company wants to assign 14 employees to 10 offices. There are four offices that require 2 people. Each 44 employee has given their preference. A1 means first choice 2 means second choice, etc. How should the 45 company assign the people to the offices to optimize the preferences of the employees? 46 47 Solution 48 1) The vonables are the assignments of the people to different offices. On worksheet Offices these are 49 given the name Assignments 50 2) There are the following logical constraints 51 Assignments - binary 52 and the other constraints 53 Assignments_per_employee - 1 54 Total_employees. Required_employees 55) The objective is to optimize the preference of the employees. That means we have to minimize the sum 56 of the total preferences given to the assigned offices, defined on the worksheet as Total_preference 57 58 Remarks 59 When everybody wants a different office there will be no problems. If all employees prefer the same 80 office (more likely. The problem gets more difficult and it might be necessary to give an employee 7th or 61 on choice it might be wise in that case to add a constraint to say that no assignment worse than 5th 62 choice is given for instance. This may cause the problem to be inteasible ie, there is no possible 63 solution this topper, you will have to relax the constraint on the assignments, eg no worse than 6th 54 or even 7th choice Summary Crew Offices Sched Sched2 Sched Hire fire Troc Type here to search o BE PROTECTED VIEW Be Careful--files from the Internet can contain viruses. Unless you need to edit 1 'Personnel scheduling for an Amusement Park 1 B C D E F G H 1 K L M N Personnel scheduling for an Amusement Park 1 For employees working five consecutive days with two days off, find the schedule 3 which meets demand from attendance levels while minimizing payroll costs 6 Sch Days off Employees A anaiMemory 3 8 B Monday Tuesday 5 9 Cinesday Wed 6 10 D Wed Thursday 4 TE Thursday Friday 6 12 F Friday Saturday 1 13 G Saturday Sunday 0 15 Schedule Totals 25 Sun Mon Tue Wed Thu Fri Sal 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 O 0 0 1 1 1 1 1 0 22 17 14 15 15 18 24 17 Total Demand 22 17 13 14 15 18 24 19 Pay/Employee/Day $40 20 Payroll/Week $5,000 21 22 23 Problem 24 An amusement park needs a certain number of employees each day of the week 25 Every employee must be on a schedule that gives him/her two consecutive days of 26 How many employees should the park hire and what schedule should they be on to 27 minimize total payroll cost? 28 29 Solution 301) The variables are the number of people hired for each of the 7 possible schedules 31 on worksheet Sched these are given the name Employees_per_schedule 32 2) The logical constraints are 83 Employees_per_schedule >=0 via the Assume Non-Negative option 34 Employees_per_schedule - integer 35 There is also the constraint to have enough employees to operate the rides each day 36 Employees_per_day>- Required_per_day 875) The objective is to minimize payroll. This is defined on the worksheet os Payroll 88 39 Remarks 40 This is an example of a simple but classic personnel scheduling problem Hospitals 41 schools, police forces, etc. can all use a model like this to optimize their personnel Summary Crew Offices Sched1 Sched2 Sched3 42 scheduling Hirefire Troop Type here to search