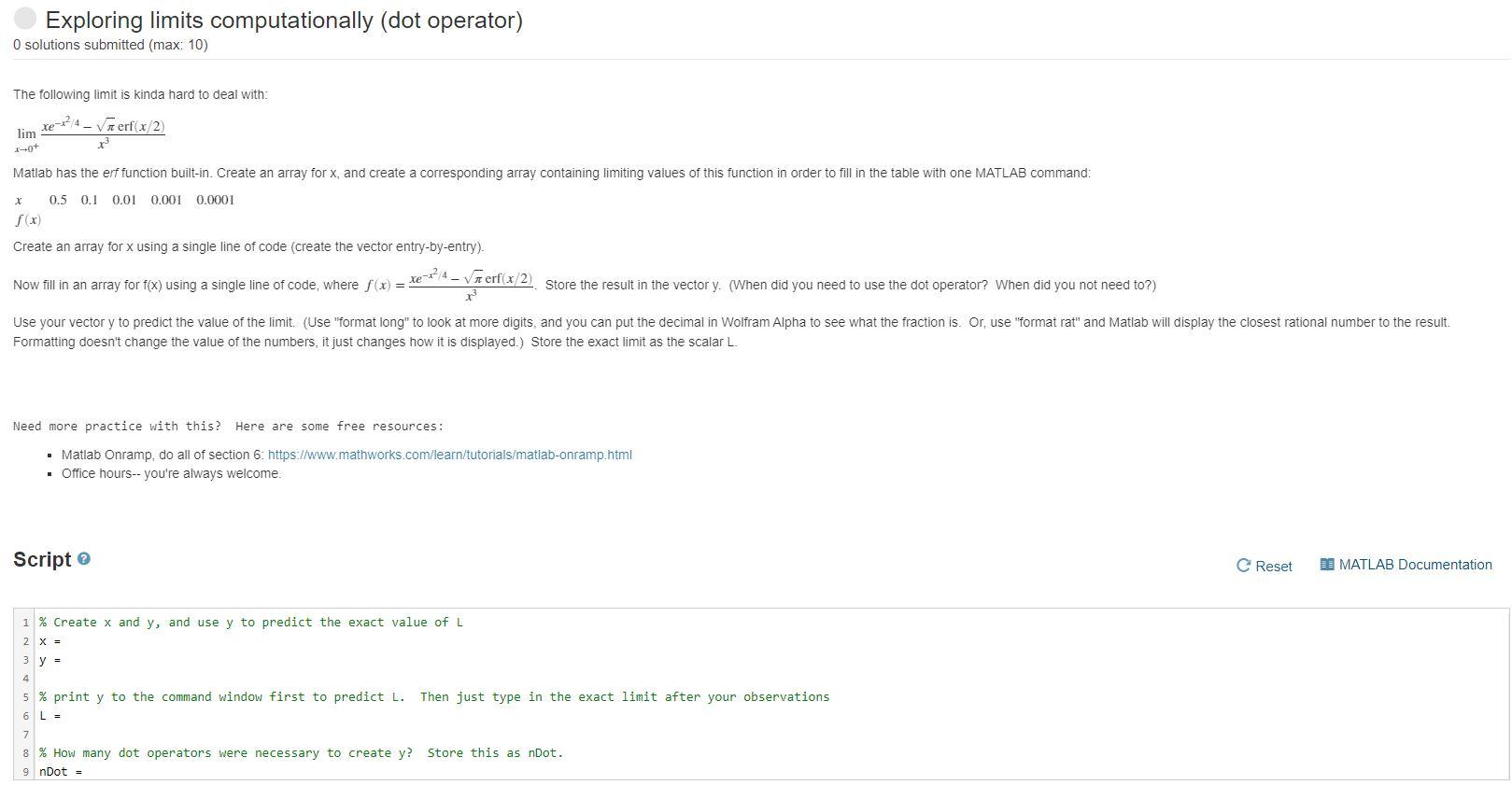
Exploring limits computationally (dot operator) O solutions submitted (max: 10) The following limit is kinda hard to deal with: xe-4 - VTerf(x2) lim x 10+ Matlab has the erf function built-in. Create an array for x, and create a corresponding array containing limiting values of this function in order to fill in the table with one MATLAB command: 0.5 0.1 0.01 0.001 0.0001 f (x) x Create an array for x using a single line of code (create the vector entry-by-entry). Now fill in an array for f(x) using a single line of code, where f(x) = xe-?4 Verf(x/2) Store the result in the vector y. When did you need to use the dot operator? When did you not need to?) Use your vector y to predict the value of the limit. (Use "format long" to look at more digits, and you can put the decimal in Wolfram Alpha to see what the fraction is. Or, use "format rat" and Matlab will display the closest rational number to the result. Formatting doesn't change the value of the numbers, it just changes how it is displayed.) Store the exact limit as the scalar L. Need more practice with this? Here are some free resources: Matlab Onramp, do all of section 6: https://www.mathworks.com/learn/tutorials/matlab-onramp.html Office hours-- you're always welcome. Script C Reset DE MATLAB Documentation 1 % Create x and y, and use y to predict the exact value of L X = 3 y = 4 5 % print y to the command window first to predict L. 6 L = Then just type in the exact limit after your observations 7 8 % How many dot operators were necessary to create y? Store this as nDot. 9 nDot =