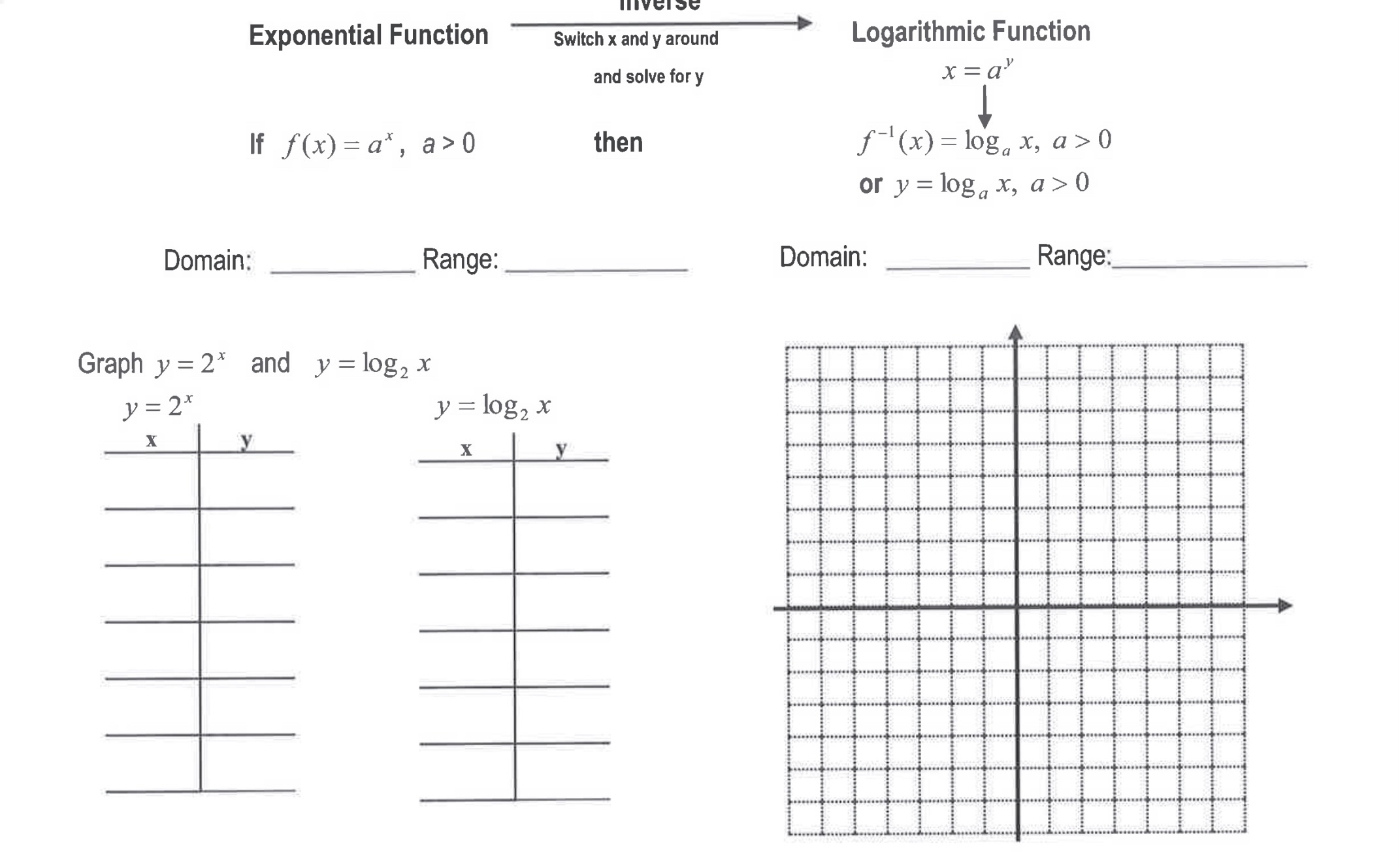
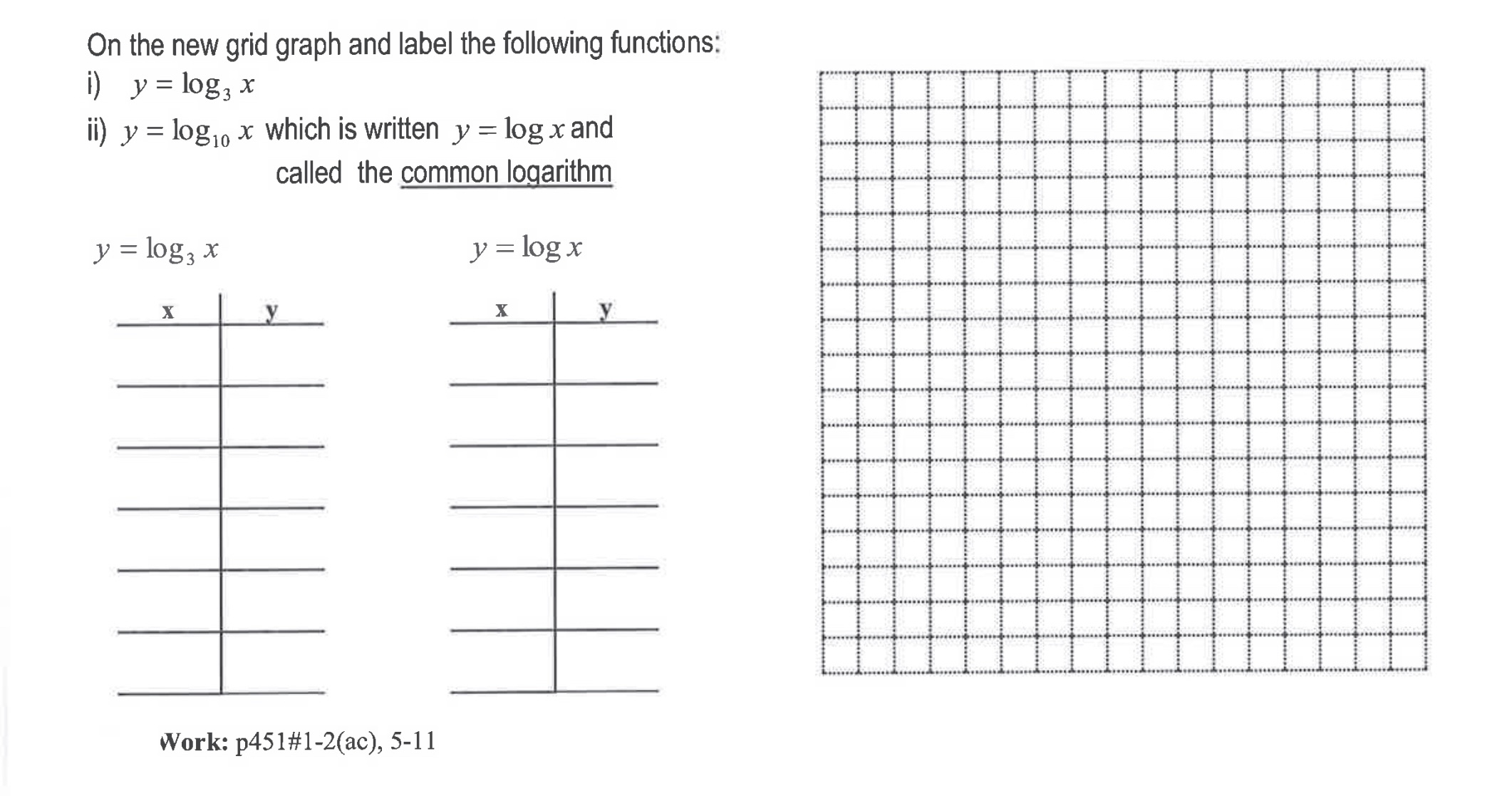
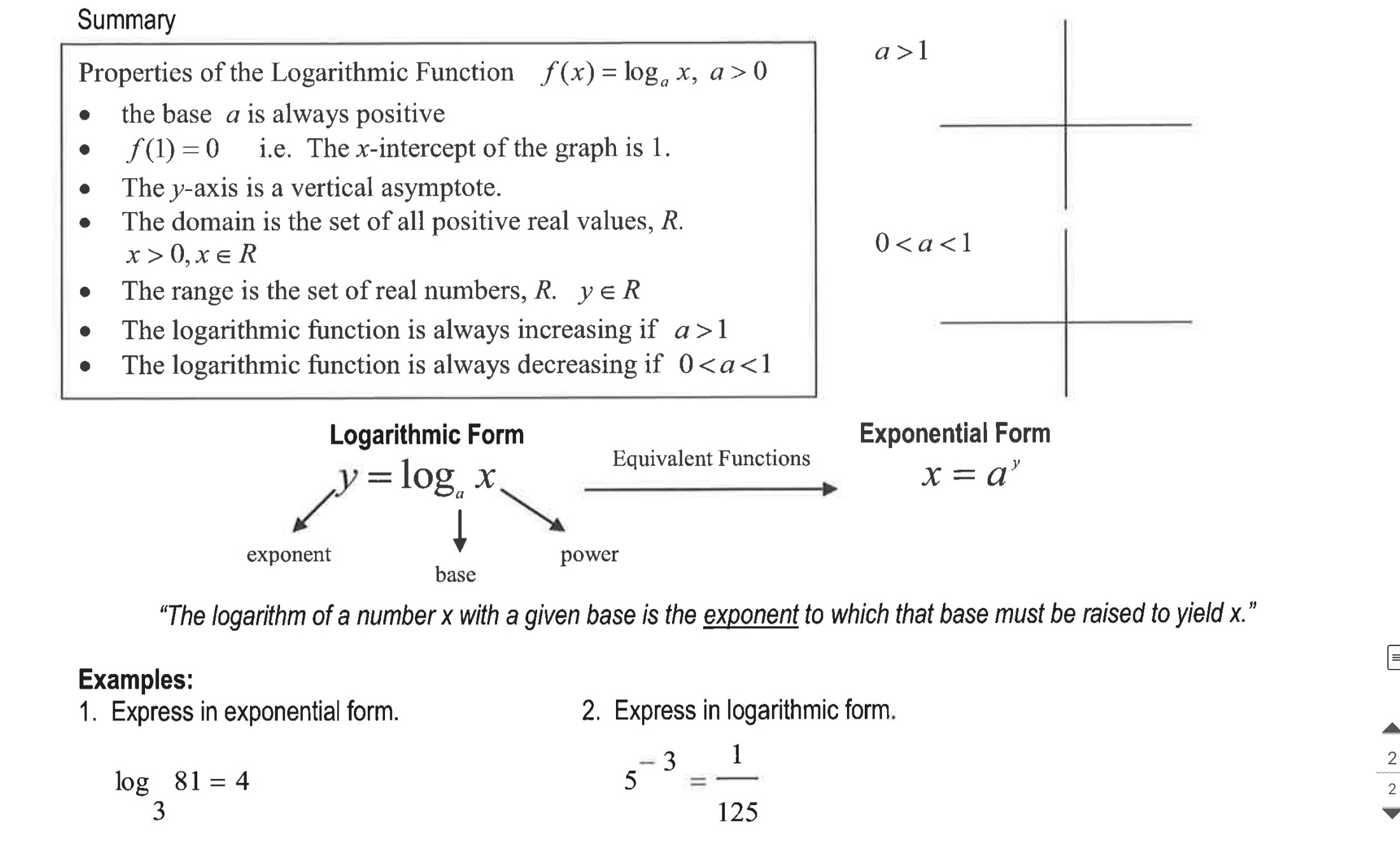
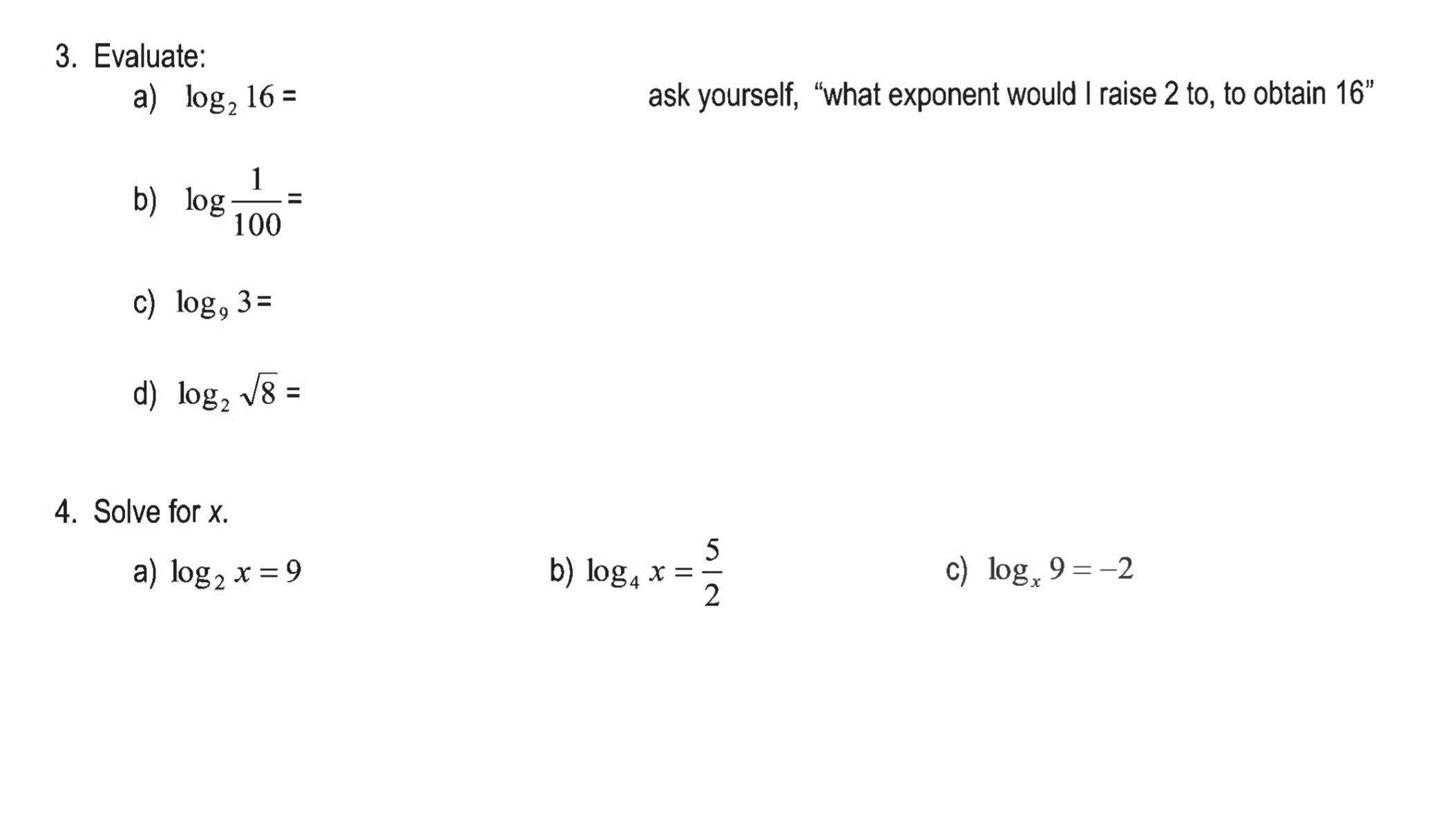
Exponential Function Switch x and y around Logarithmic Function and solve for y x = a If f ( x) = a*, a>0 then f-' (x) = log, x, a>0 or y = log x, a > 0 Domain: Range: Domain: Range: Graph y = 2* and y = log, x y = 2* y = log2 XOn the new grid graph and label the following functions: i) y = log, x ii) y = log1 x which is written y = log x and called the common logarithm y = log3 x y = log x Work: p451#1-2(ac), 5-11a >1 Properties of the Logarithmic Function f (x) = log\" x, a > 0 the base a is always positive f (1) = 0 Le. The xintercept of the graph is 1. The yaxis is a vertical asymptote. The domain is the set of all positive real values, R. x > 0, x e R 0 1 The logarithmic function is always decreasing if 0