Exponential growth functions increase at an increasing rate. We can observe this by calculating the average rate of change on different intervals of the function. [You may want to refer to Section 2.4 to review average rate of change].

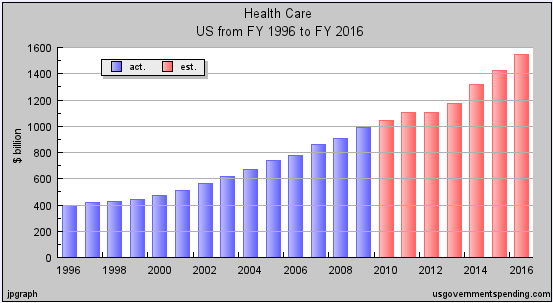
The graph models healthcare spending by the U.S. Government.

Estimating from the graph, it would appear they-value is 1580 in 2016, 790 in 2006, and 400 in 1996.

We first calculate the slope of the straight line that would connect the points (1996,400) and (2006,790).

(790 - 400)/(2006 - 1996) = 390/10 = 39 billion dollars per year.

Now the slope of the straight line that would connect the points (2016,1580) and (2006,790).

(1580 - 790)/(2016 - 2006) = 790/10 = 79 billion dollars per year.

These areaverage annual rates of change. Theaverage annualincreasein health care expense went from $39 billion per year on the interval (1996,2006) to $79 billion per year on the interval (2006,2016).The rate of increasedoubled.

Health Care US from FY 1996 to FY 2016 1600 act. est. 1400 1200 1000 $ billion 800 600 400 200 1996 1998 2000 2002 2004 2006 2008 2010 2012 2014 2016 jpgraph usgovernmentspending.com