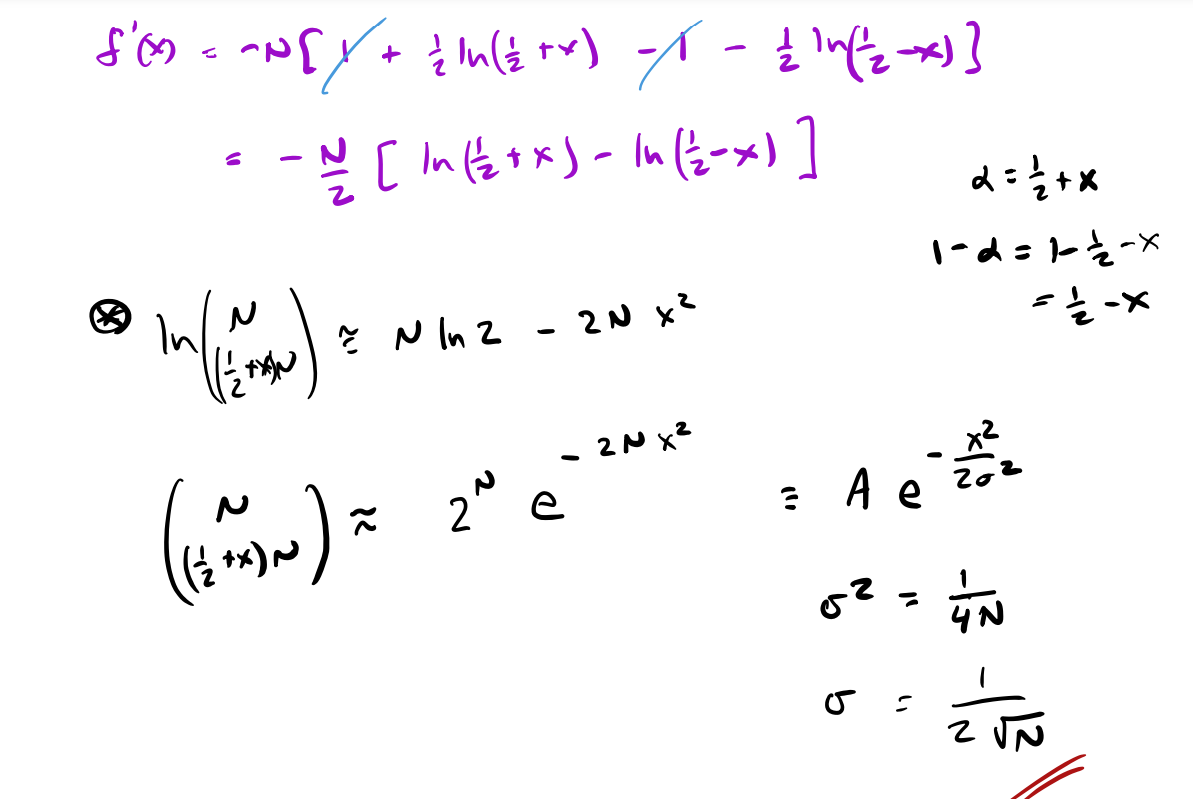
Extra stuff: let's confirm what you learned on the last page analytically. (a) To get a better idea of how the binomial coefficients behave for large numbers, we need to obtain something called the Stirling Approximation. Start with In N! = Eli ~ dx Inx and show that In N! ~ N In N - N. This is the lowest order Stirling approximation. (ex inx xin x lo - Sax = NMUN - N odv u (b) Consider now In (a ) where a is between 0 and 1. Use the Stirling approximation to approximate this quantity when N is large. In (N) = In N! : Nink - 25 -2NindN + dro - (1- 2)N la (1-2)N ( dN) ! ( N - dN ) ! + 1 1 - 2) N = NIKN - anthN -(N-IN)InN - awind - (1-2)Nin(1-a) = - N [alua + (1-2) In (1-d) ] dod No ( Ina - Inchd ) - - N / 1 + (a * ! ) edit = - 4N