f is a twice-differentiable function defined on the interval [-2.25, 2.25] with f(0) = 5.

The graph of f ?, the derivative of f, is shown in the attachment. The areas of the regions bounded by the x-axis and the graph of f ? on the intervals [-2, -1], [-1, 0], [0, 1], and [1, 2] are 6, 4, 4, and 6 respectively.

a) Determine the critical points of f and classify each as a relative minimum, relative maximum, or neither. Justify your answer.

b) Is there a value of c on the interval [0, 2], such that ?(?) = 4? Justify your answer.

c) Write an expression for f(x) that involves an integral. Find all x-coordinates, besides x = 0, for

which f(x) = 3. Justify your answer.

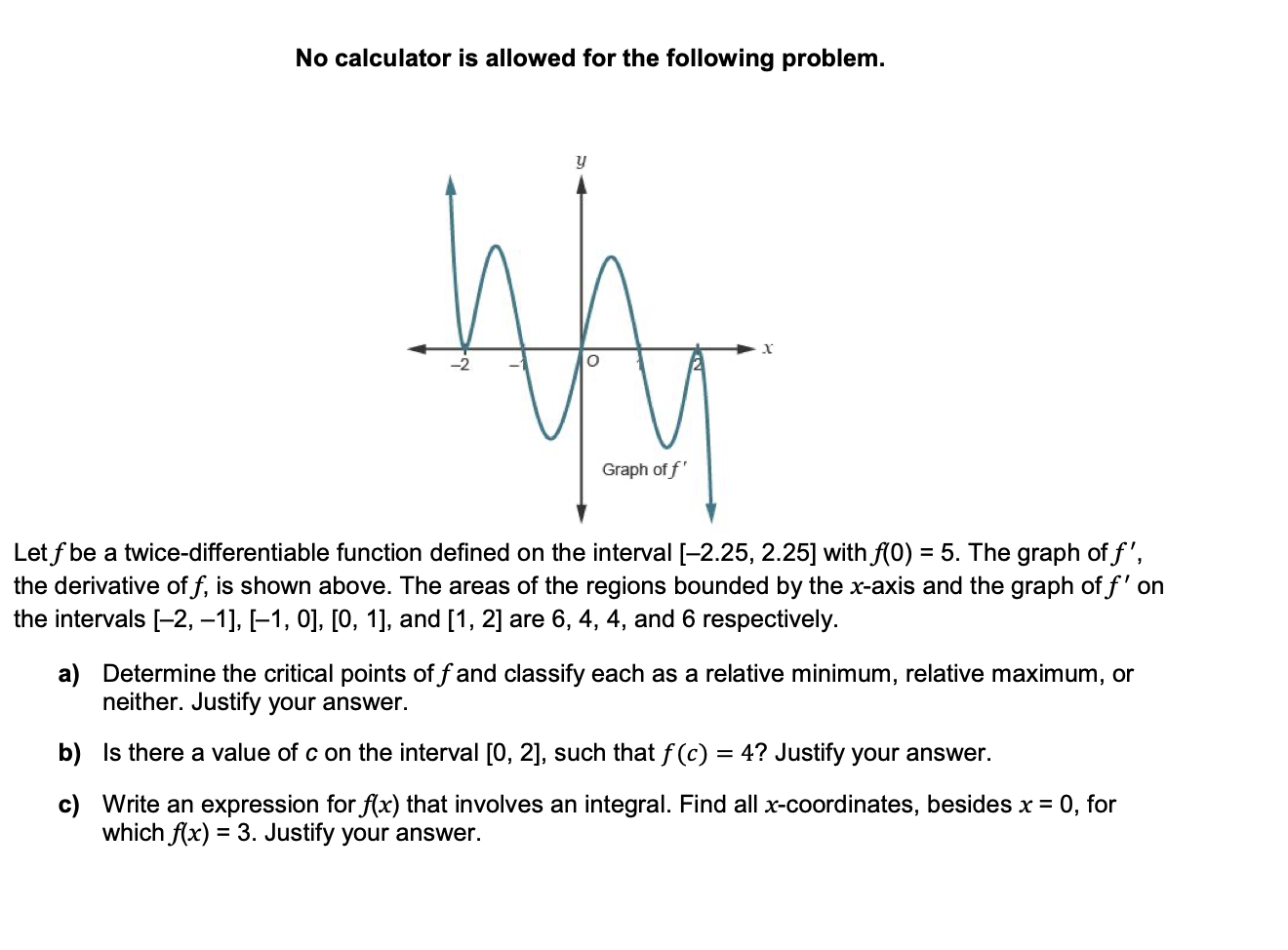
No calculator is allowed for the following problem. Graph of f ' Let f be a twice-differentiable function defined on the interval [2.25, 2.25] with O) = 5. The graph off', the derivative off, is shown above. The areas of the regions bounded by the x-axis and the graph off' on the intervals [2, 1], [1, 0], [0, 1], and [1, 2] are 6, 4, 4, and 6 respectively. a) Determine the critical points of f and classify each as a relative minimum, relative maximum, or neither. Justify your answer. b) Is there a value of c on the interval [0, 2], such that f (c) = 4? Justify your answer. c) Write an expression for x) that involves an integral. Find all xcoordinates, besides x = 0. for which x) = 3. Justify your