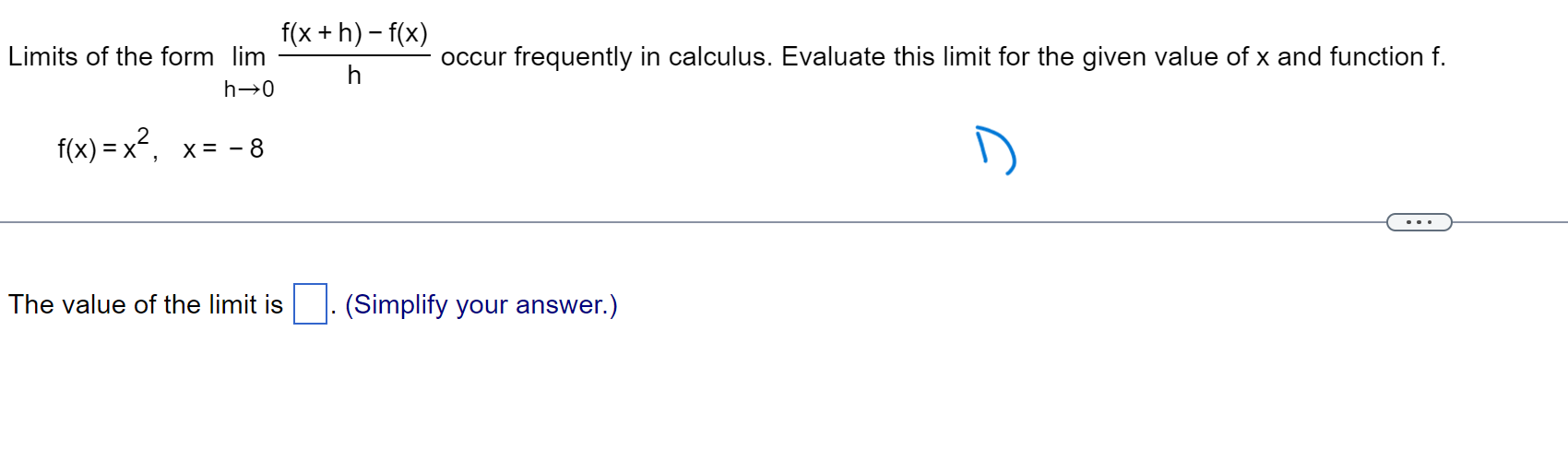
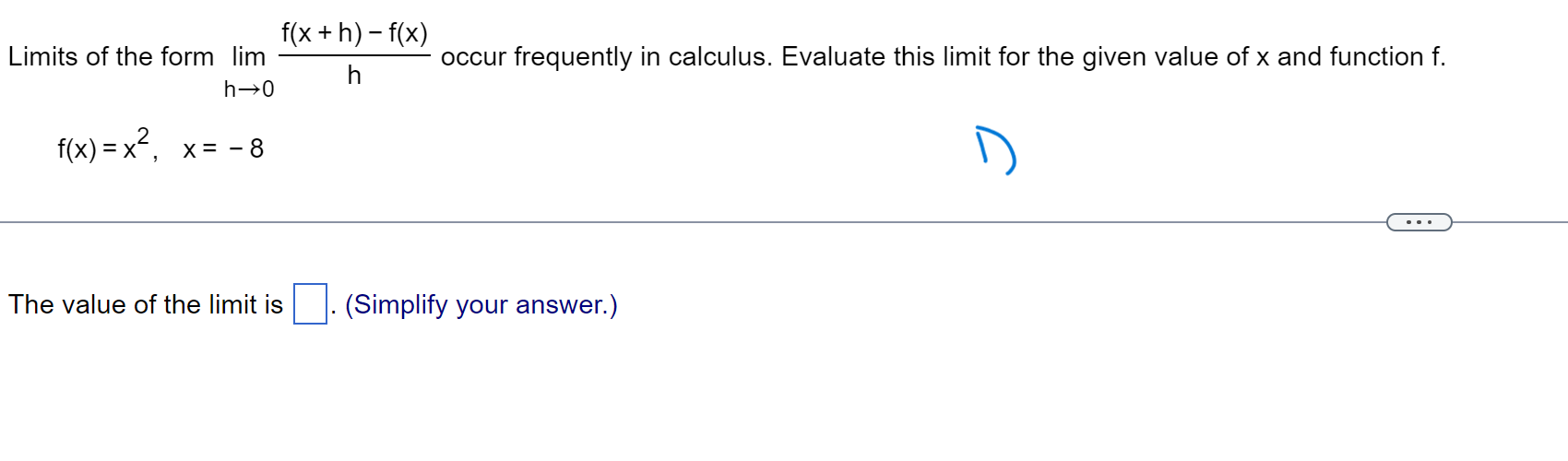
Question: f ( x + h) - f(x) Limits of the form lim h occur frequently in calculus. Evaluate this limit for the given value of

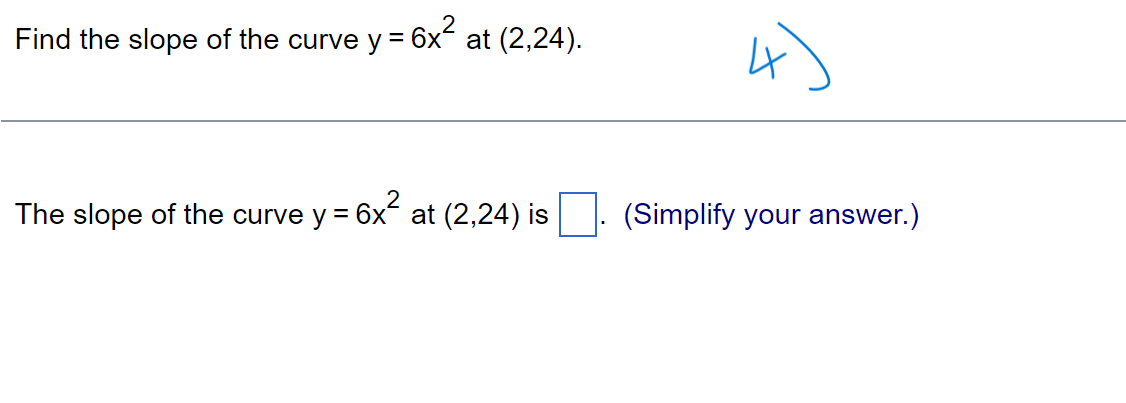






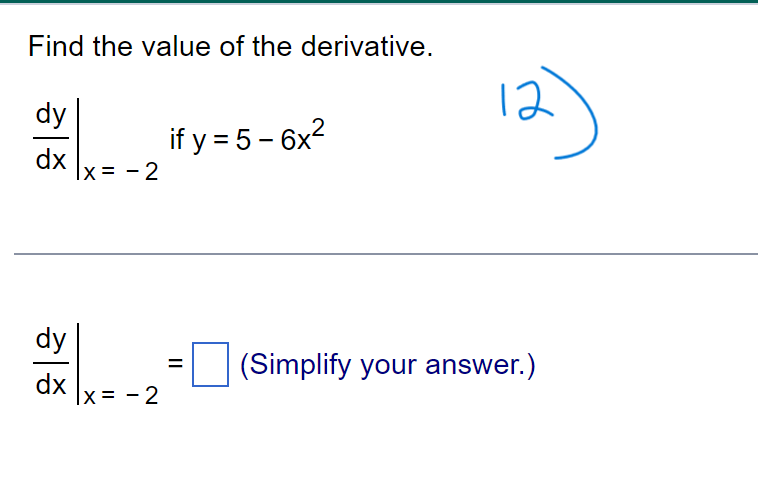
![[2,12] TIL AR 3 E = D (Simplify your answer.) Use a](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66644a94badc4_72466644a94a813a.jpg)
![curve and the x-axis on the interval [0, b]. ii) y=9x2 The](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66644a9589b85_72566644a9566d82.jpg)
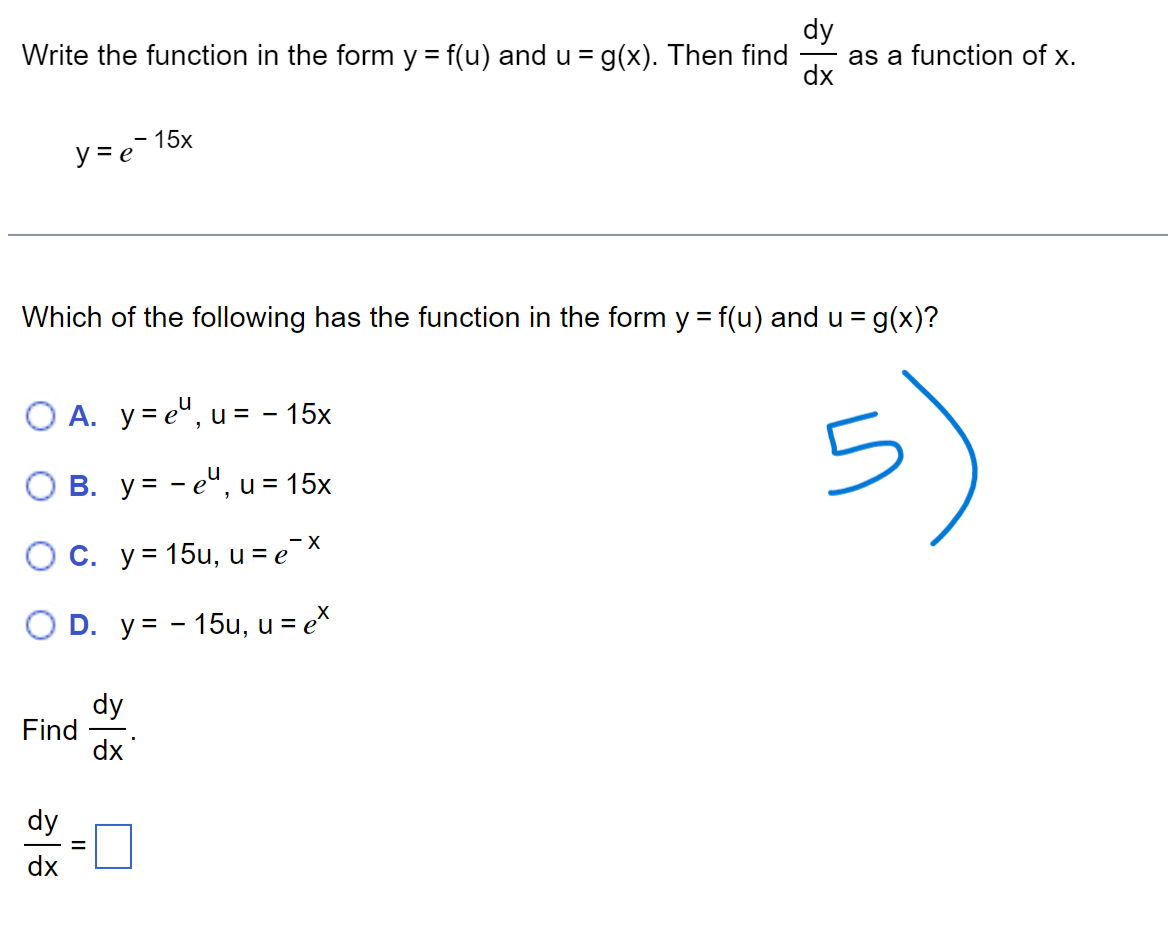






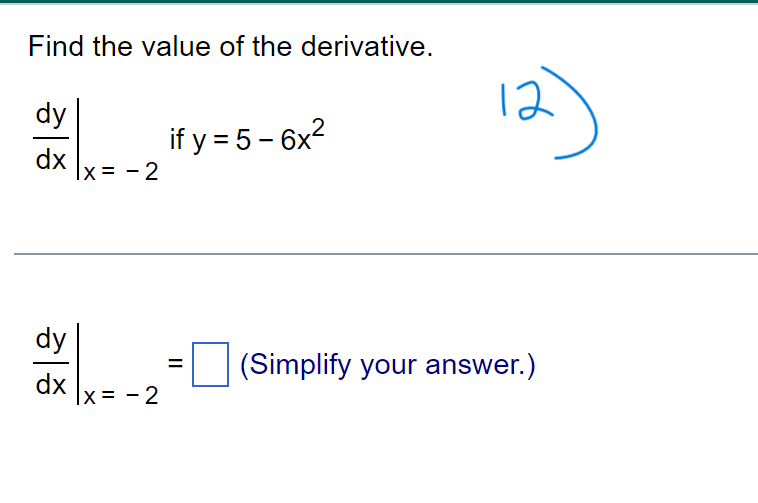
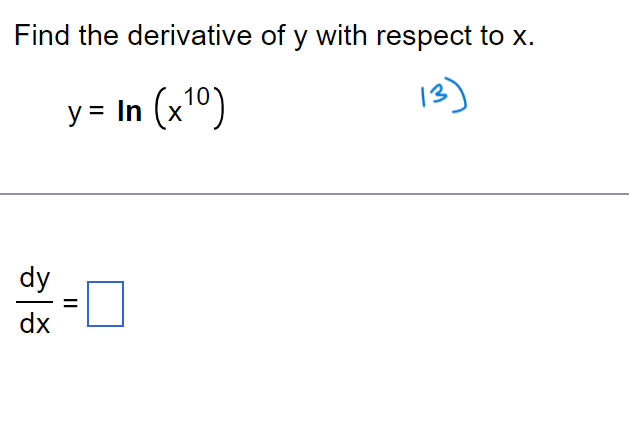
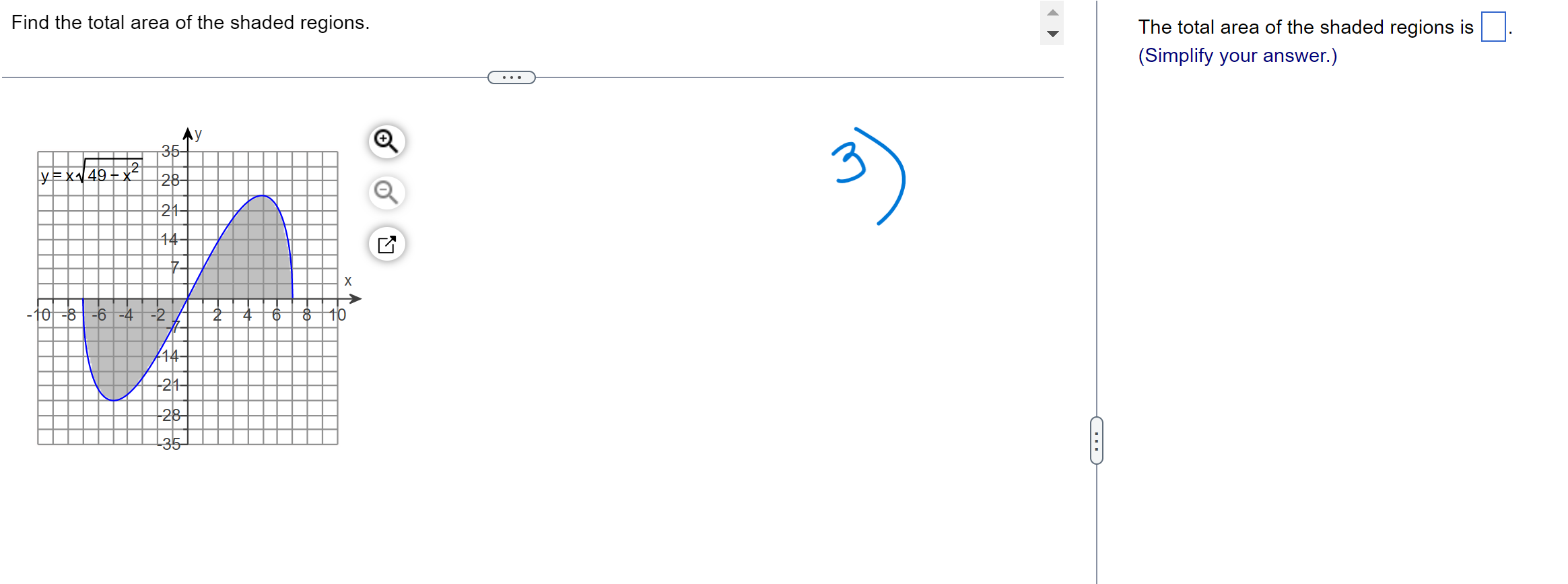
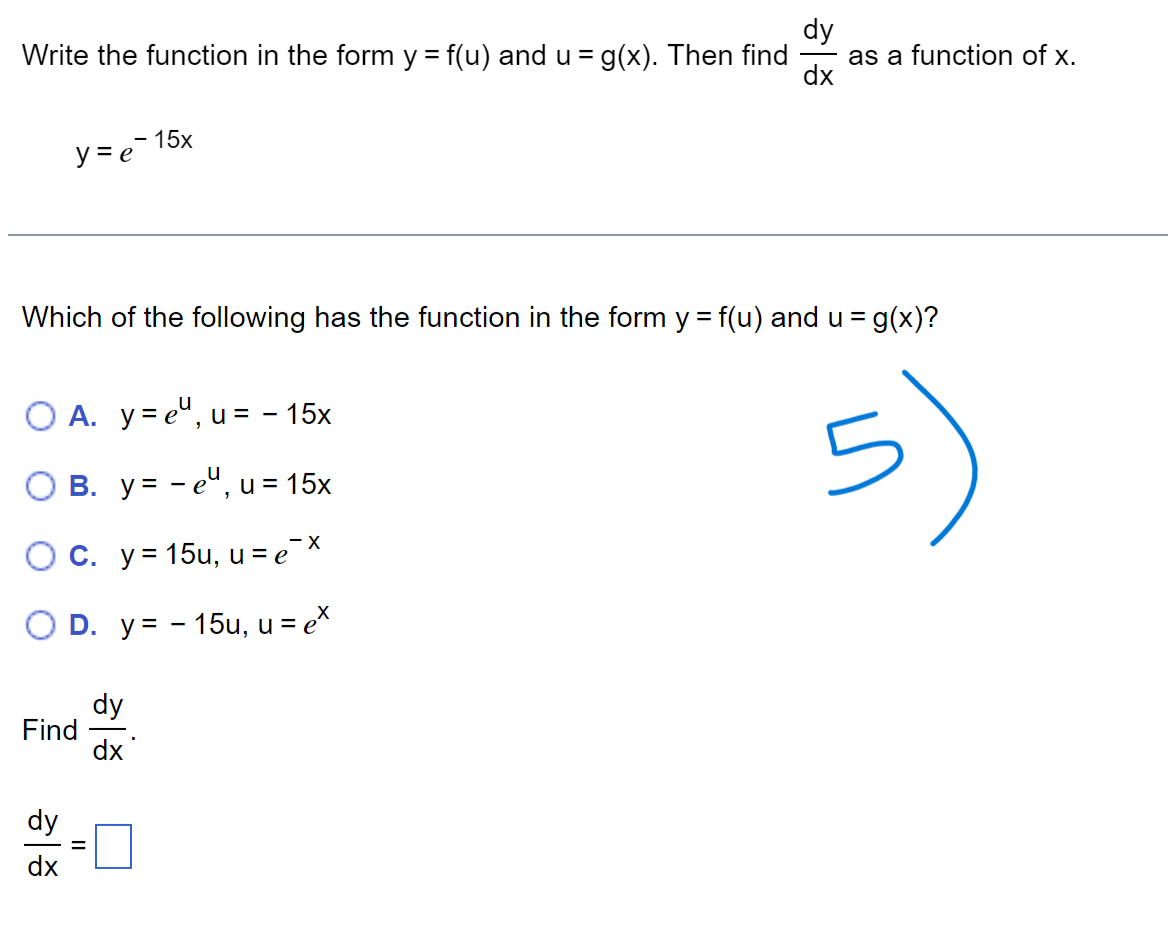
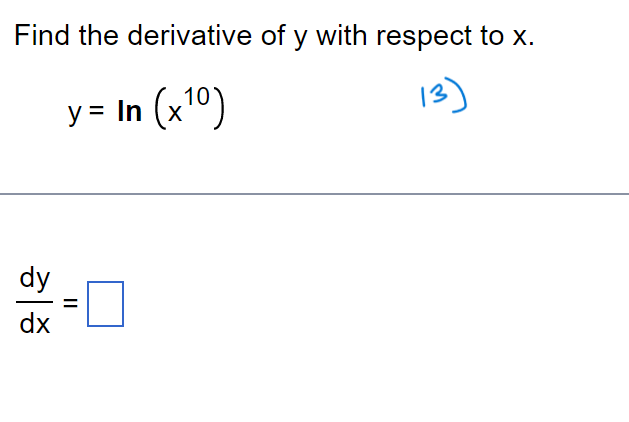
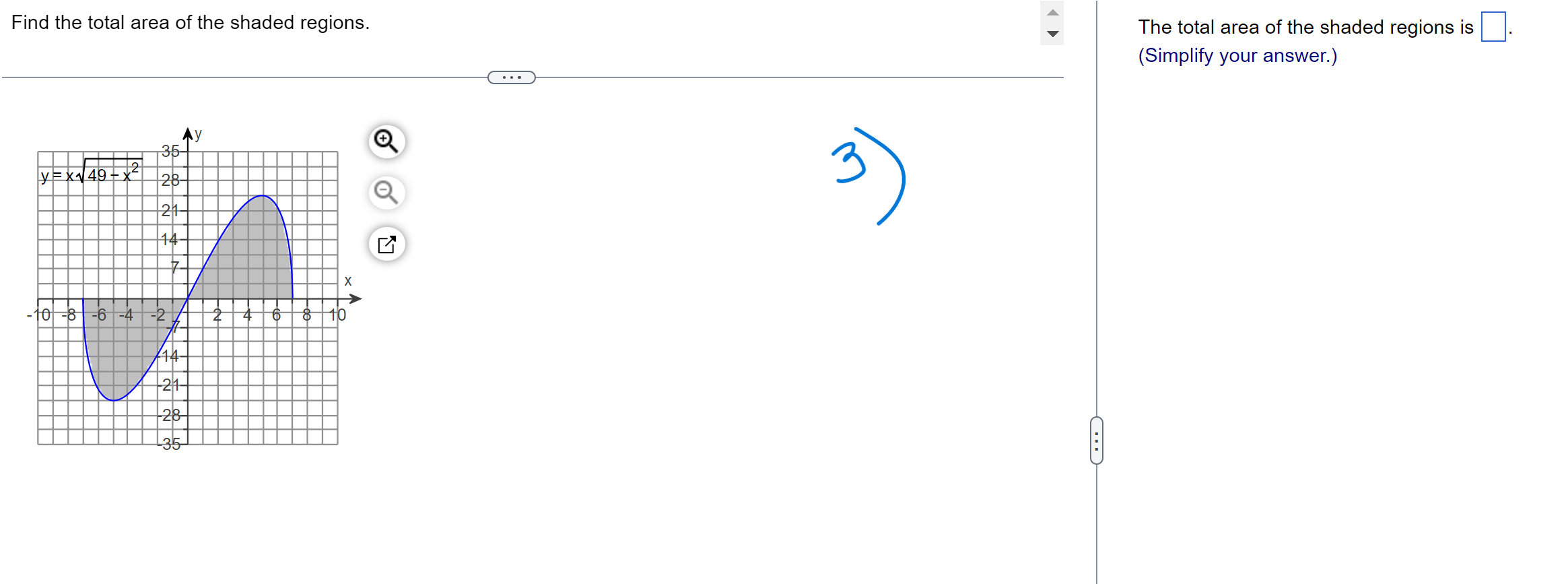
f ( x + h) - f(x) Limits of the form lim h occur frequently in calculus. Evaluate this limit for the given value of x and function f. h -0 f ( x) = X, x= - 8 . . . The value of the limit is . (Simplify your answer.)\f> Find the total area of the shaded regions. The total area of the shaded regions is D. (Simplify your answer.) 4 Find the slope of the curve y = 6x2 at (2,24). Dr\\ The slope of the curve y = 6x2 at (2,24) is D. (Simplify your answer.) dy Write the function in the form y = f(u) and u = g(x). Then find a as a function of x. y=e-15x Which of the following has the function in the form y = f(u) and u = 900? U {:3 A. y=e ,u= 15x in) B. y= -e\\fFind the average rate of Change of the function over the given interval. R(8) = J49 +1 ; [2,12] TIL AR 3 E = D (Simplify your answer.) Use a definite integral to find the area of the region between the given curve and the x-axis on the interval [0, b]. ii) y=9x2 The area is D. \fFind the value of the derivative. dy 12 if y = 5 - 6x2 dx Ix= - 2 dy (Simplify your answer.) dx x= - 2
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


