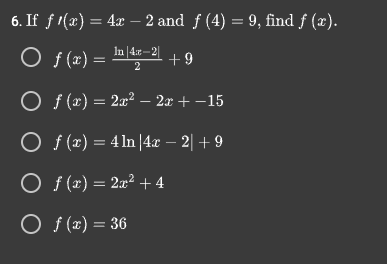
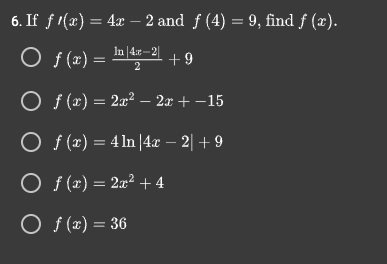
\f1. Considering the differential equation # = 7y + 3 with initial condition (0, 5), solve for y. Oy= -380 72 + 3 Oy= -19e 12 - 3 O y= 7el + 41 O y= 3Be 7 3 2. If de dy - 14 - 2 = 0, and y(0) = 7, then y = * + 2x + 7. O True O False 3. Solve the differential equation y/ = Sy, with y(0) = -4. Oy=e 8 - 4 Oy= -8x - 4 Oy= -4In(8x) Oy= -4e Bar Oy= -$+32 4. The function y = Cest - 10 solves the differential equation y/ - 6y/ = -5y - 50. O True O False 5. Solve the differential equation * = 7re, with the initial condition (0, 0). Oy= -7: Oy= - In(1 -72) Oy= In(2) - 141n(x) Oy= - In(1 - 123) Oy= -15