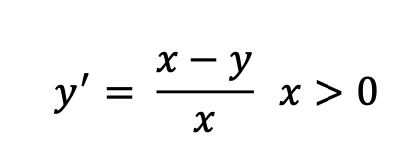
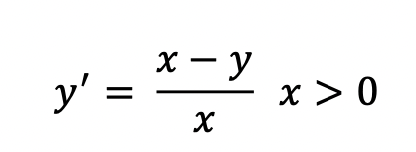
\f1. First, show that this differential equation is exact. Then solve it by using the method of exact differential equation that we learned in class. That is, find the potential function and then write the general solution of the differential equation. Finally, solve the general solution for \"y\" and write your final answer in explicit form. You may replace |x| = x since 36 > 0. 2. Show that the same differential equation is also linear by writing it in the format: 37' + py = q. Then use the techniques of solving a linear differential equation. Find the integrating factor (you may replace IxI = x since x > 0) and use the formula we learned in class for linear first-order differential equations. Do you get the same answer as #1? 5. Use GeoGebra. Create a slider for "a". Then enter the specific solution you find in problem 4. Move your slider. What do you notice? Is there a specific value of "a" when the behavior of the graph changes? What is that value of "a"? Screen shot three graphs of the specific solution: one for a > 1/2, one for a = 1/2 and one for a