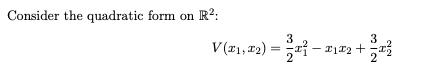
\fa) Obtain the symmetric matrix M such that V(x) = = Mr. b) Obtain the coordinate transformation matrix P such that expressed with respect to the new coor- dinates a = P-x, V(@) = A where A is a diagonal matrix. c) The level curve of V is the set {r e R' | V(x) = c}. Use the simpler diagonal representation to draw the level curve for c = 1. Indicate the following two sets: {rER' [ V(x) c) d) Consider now the general case V(x) = cMr on R' where M is a symmetric matrix with eigenvalues 1 and 12. What can be said about the shape of the level curve and the other two sets in the following two cases: Case I: A >0, > >0 Case II: Al 0 e) Consider now a positive definite quadratic form on R", V(x) = c' Me. What is the shape of the level curve in R"? Indicate also the two sets in the equations above