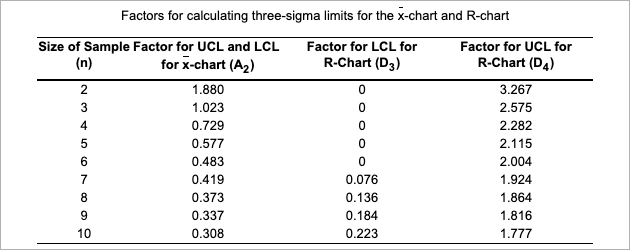
Question: Factors for calculating three-sigma limits for the x-chart and R-chart Factor for LCL for R-Chart (D3) Size of Sample Factor for UCL and LCL for

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


