Question: f(b}- [(3) b _ a = f'tc) in the conclusion of the mean value theorem for the function and interval shown below. Find the value
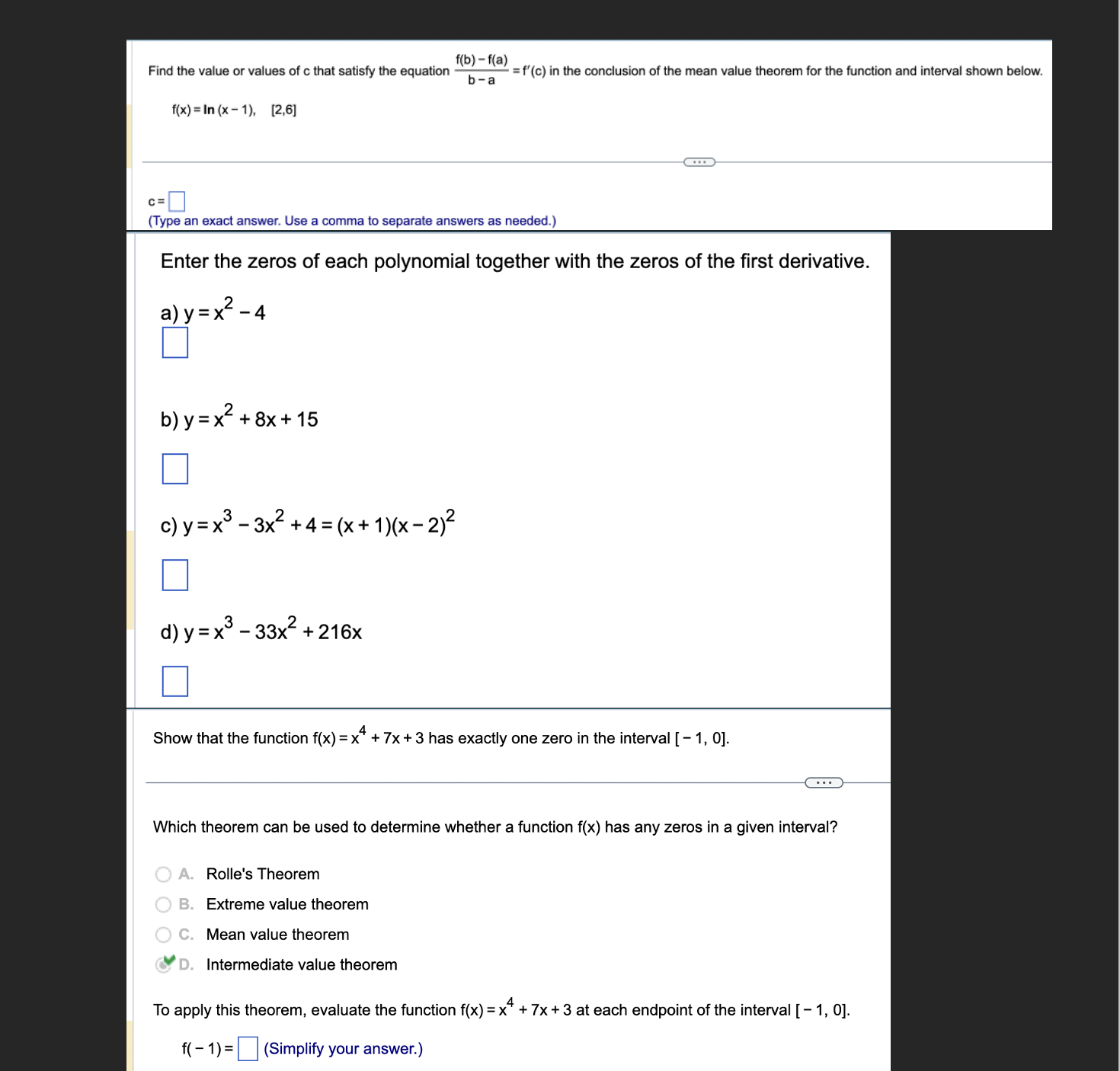
![the value or values of c that satisfy the equation f{x)=|n{x-1), [2.5]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66799ac33beae_50766799ac31cd0c.jpg)
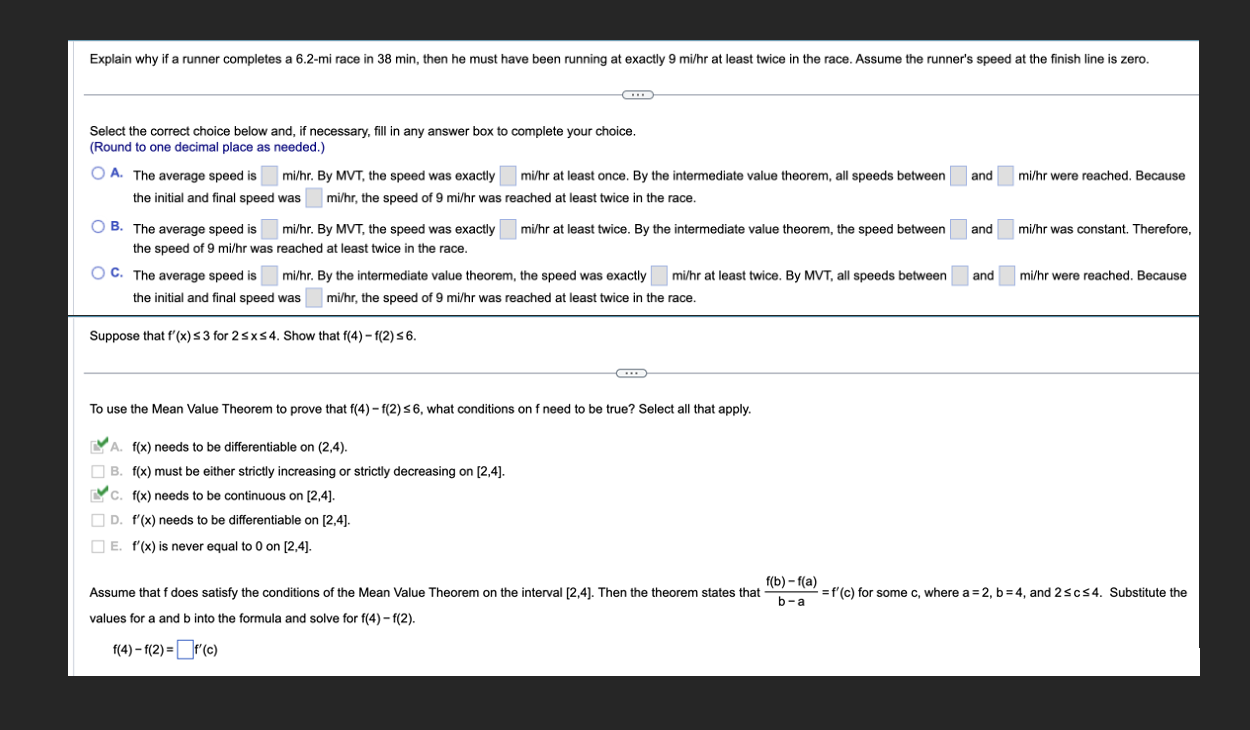
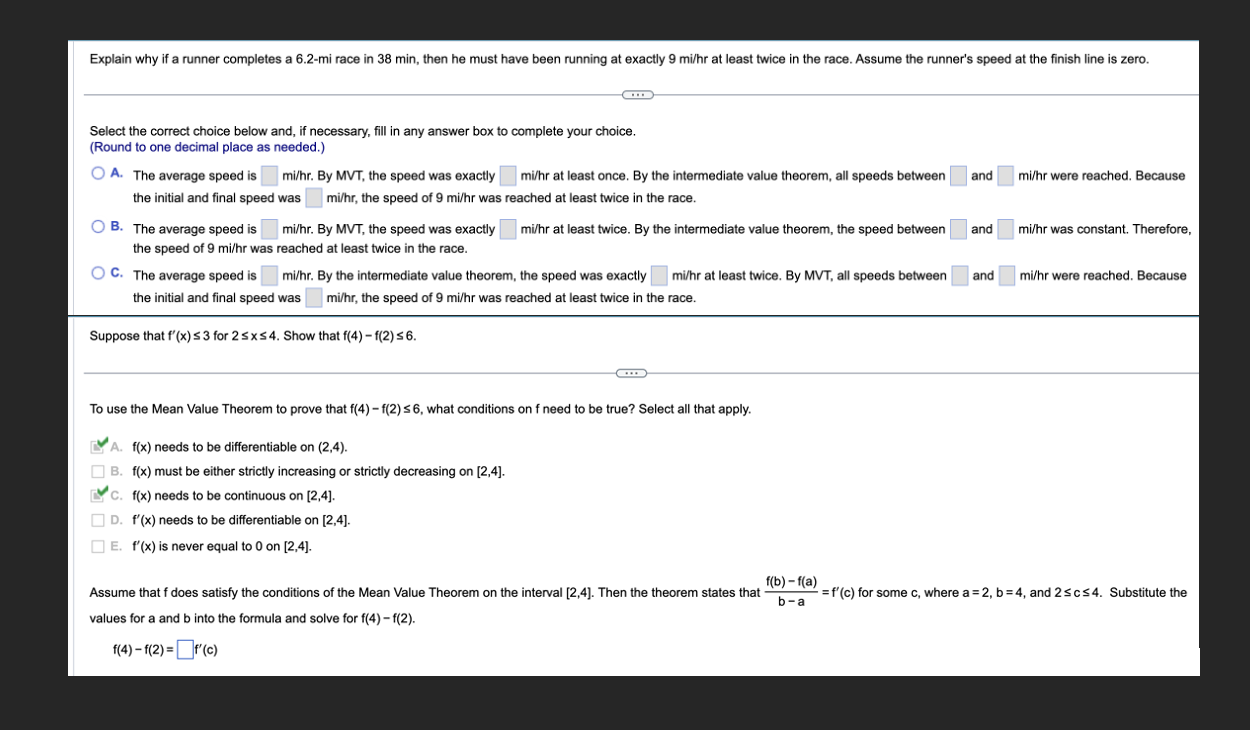
f(b}- [(3) b _ a = f'tc) in the conclusion of the mean value theorem for the function and interval shown below. Find the value or values of c that satisfy the equation f{x)=|n{x-1), [2.5] a? {Type an exact answer. Use a comma to separate answers as needed.) Enter the zeros of each polynomial together with the zeros of the first derivative. 2 a)y=x 4 D b)y=x2+8x+15 D c)y=x3-3x2+4=(x+1)(x-2)2 D d)y=x3 -33x2+216x D Show that the function {(x) = x4 + 7x + 3 has exactly one zero in the interval [ 1, O]. Which theorem can be used to determine whether a function f(x) has any zeros in a given interval? Rolle's Theorem Extreme value theorem Mean value theorem Intermediate value theorem To apply this theorem, evaluate the function f(x) = x4 + 7x + 3 at each endpoint of the interval [-1, O]. f(-1)= D (Simplify your answer.) Explain why if a runner completes a 6.2-mi race in 38 min, then he must have been running at exactly 9 mi/hr at least twice in the race. Assume the runner's speed at the finish line is zero. Select the correct choice below and, if necessary, fill in any answer box to complete your choice. (Round to one decimal place as needed.) O A. The average speed is mi/hr. By MVT, the speed was exactly mi/hr at least once. By the intermediate value theorem, all speeds between and mi/hr were reached. Because the initial and final speed was mi/hr, the speed of 9 mi/hr was reached at least twice in the race. O B. The average speed is mi/hr. By MVT, the speed was exactly mi/hr at least twice. By the intermediate value theorem, the speed between and mi/hr was constant. Therefore, the speed of 9 mi/hr was reached at least twice in the race. O C. The average speed is mi/hr. By the intermediate value theorem, the speed was exactly mi/hr at least twice. By MVT, all speeds between and mi/hr were reached. Because the initial and final speed was mi/hr, the speed of 9 mi/hr was reached at least twice in the race. Suppose that f'(x) $ 3 for 2 sx $4. Show that f(4) - f(2) $ 6. To use the Mean Value Theorem to prove that f(4) - f(2) s 6, what conditions on f need to be true? Select all that apply. [Y A. f(x) needs to be differentiable on (2,4). B. f(x) must be either strictly increasing or strictly decreasing on [2,4]. [Y C. f(x) needs to be continuous on [2,4]. D. f'(x) needs to be differentiable on [2,4]. E. f'(x) is never equal to 0 on [2,4]. Assume that f does satisfy the conditions of the Mean Value Theorem on the interval [2,4]. Then the theorem states that- atf(b) -f(@) b-a = f'(c) for some c, where a = 2, b =4, and 2 sc$4. Substitute the values for a and b into the formula and solve for f(4) - f(2). 1(4) - 1(2) = F'(c)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


