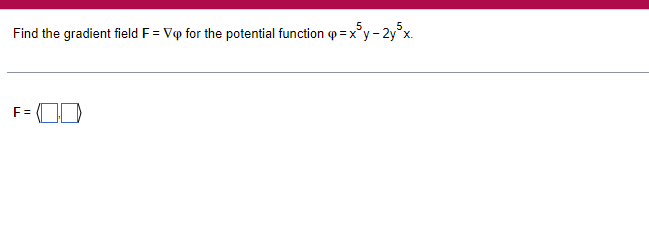
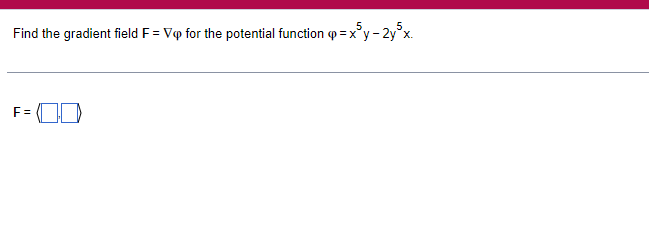
\fb Explain how a line integral differs from the single-variable integral | f(x)dx. a Choose the correct answer below. O A. A line integral is taken along an interval, an ordinary single-variable integral is taken along a curve. O B. A line integral is taken along a curve, an ordinary single-variable integral is taken along an interval. O C. A line integral is taken along a vector field, an ordinary single-variable integral is taken along a scalar field. O D. A line integral is taken along a vector field, an ordinary single-variable integral is taken along a curve