Question: Evaluate the sum 211:: [E i/k 1] = If the answer is a rational number but not an integer, type a/b, where a and b
![Evaluate the sum 211:: [\\E \\i/k 1] = If the answer](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665f90216eb7_9136665f901ee119.jpg)


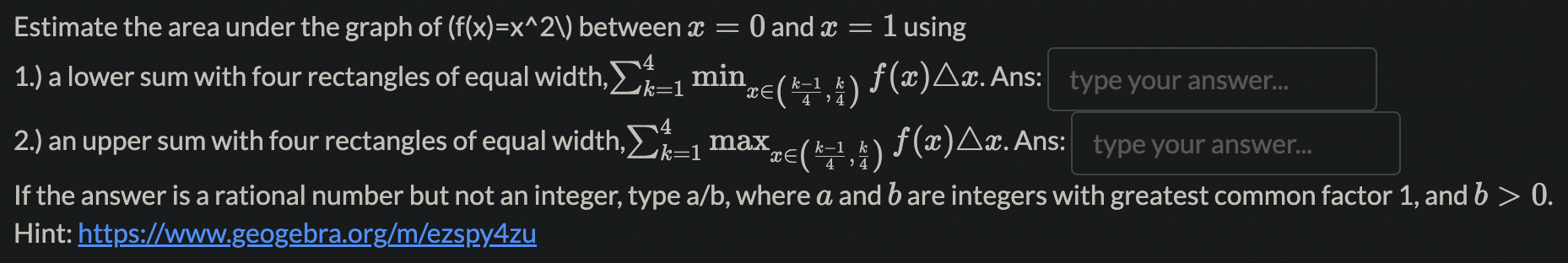



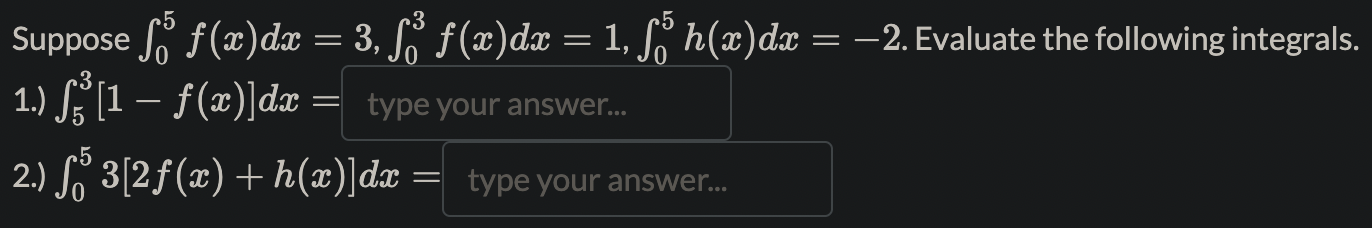



![1] and f (a) = . The Riemann sum SP = _k-1](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665f906aea15_9186665f9068c6bf.jpg)

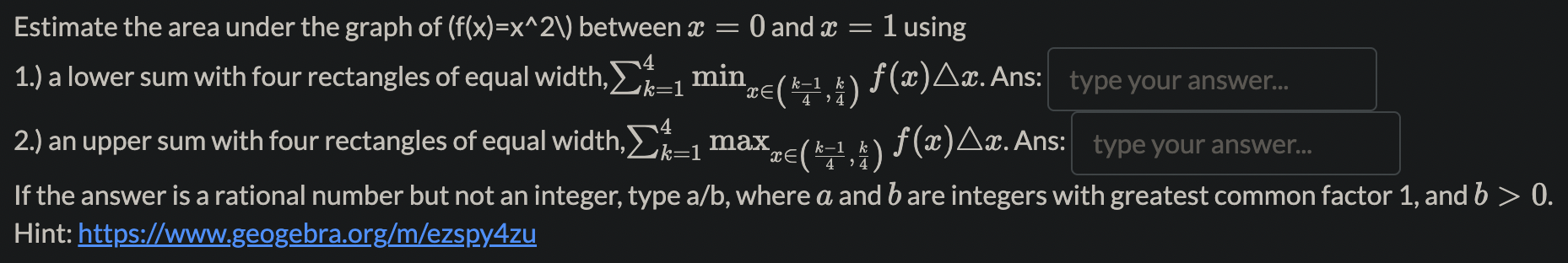



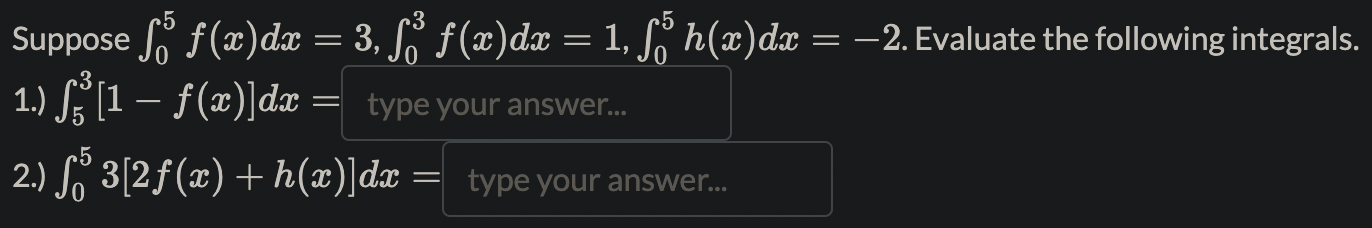

![is integrable over [a, b] for any real number a, b E](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665f909ba7de_9216665f9099e9c2.jpg)
Evaluate the sum 211:: [\\E \\i/k 1] = If the answer is a rational number but not an integer, type a/b, where a and b are integers with greatest common factor 1, and b > 0. Estimate the area under the graph of (flx)=x"2\\) between a: = 0 and a: = 1 using 1.) a lower sum with four rectangles of equal widthzi:1 mintq 1 ) f(:B)Am. Ans: 2.) an upper sum with four rectangles of equal width,Z::1 maxrE .. t) f(;1:)Aa:. Ans: . ,4 If the answer is a rational number but not an integer, type a/b, wher a and b are integers with greatest common factor 1, and b > 0. Hint: ' Let P = {0, 0.1, 0.3, 0.6, 0.9, 1} be a partition of the interval [0, 1] and f (a) = . The Riemann sum SP = _k-1 f (Ck) k Where Ck is the midpoint of each subinterval is type your answer... (give your answer to 2 decimal places). The norm of P is || P|| = type your answer... 2. . . . . The limit of the sum hmnaoo 22:1 % (E) IS . If the answer IS a rational number but not an Integer, type a/b, where a and b are Integers TL with greatest common factor 1, and b > 0. The function f (x) = x is integrable over [a, b] for any real number a, b E B with a
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


