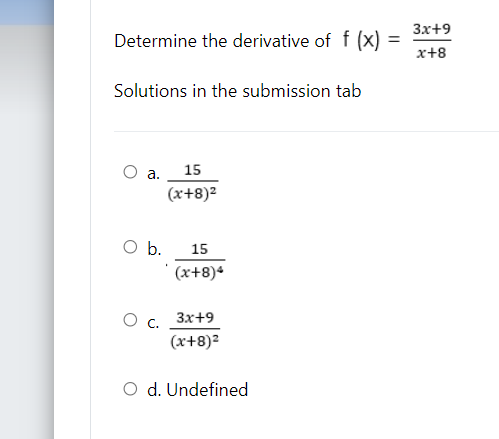
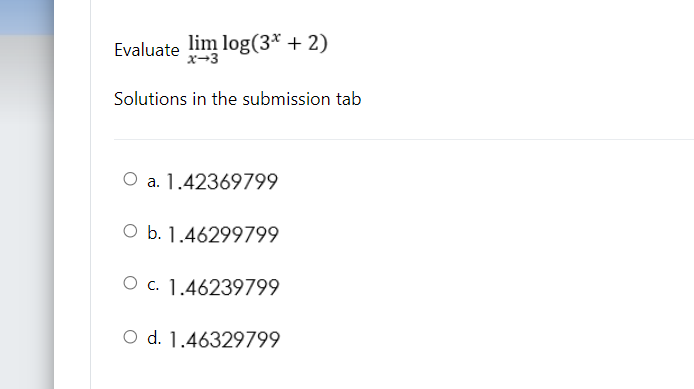
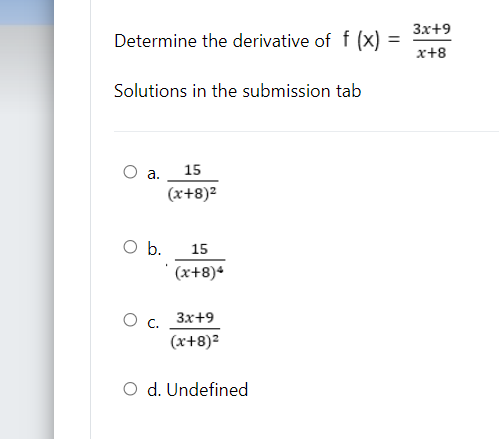
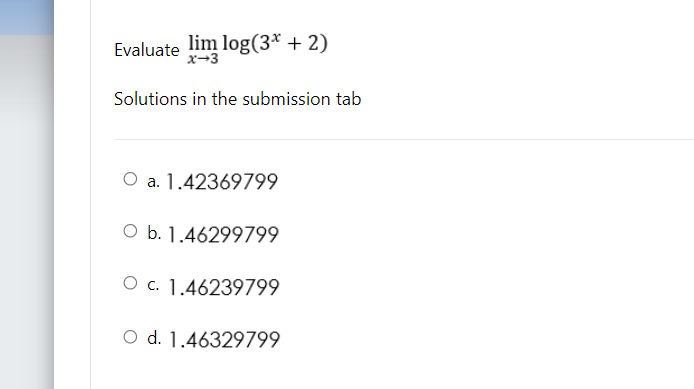
\fDetermine if the function is continuous at f (x) = x +2x+15 x-3 Solutions in the submission tab O a. Continuous at x = 5 but discontinuous at x = 3 O b. Discontinuous at x = 5 but continuous at x = 3 O c. Discontinuous at x = 5 and x = 3 O d. Continuous at x = 5 and x = 3Determine if the function is continuous at f (x) = x3+8x+16 x2-16 Solutions in the submission tab O a. Continuous at x = 4 but discontinuous at x = 2 O b. Continuous at x = - 4 and x = 4 O c. Discontinuous at x = 4 but continuous at x = - 4 O d. Discontinuous at x = 4 but continuous at x = 2x+3 Determine if the function is continuous at f (x) = x2-6x+9 Solutions in the submission tab O a. Continuous at x = 3 but discontinuous at x = - 3 O b. Discontinuous at x = 3 and x = - 3 O c. Continuous at x = 3 and x = - 3 O d. Discontinuous at x = 3 but continuous at x = - 3\fEvaluate lim ex X - 00 Solutions in the submission tab O a. Zero O b. Undefined O c. Negative infinity O d. Positive infinity