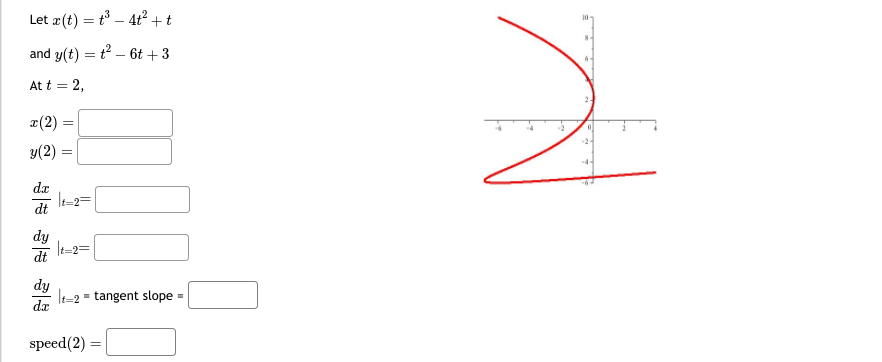
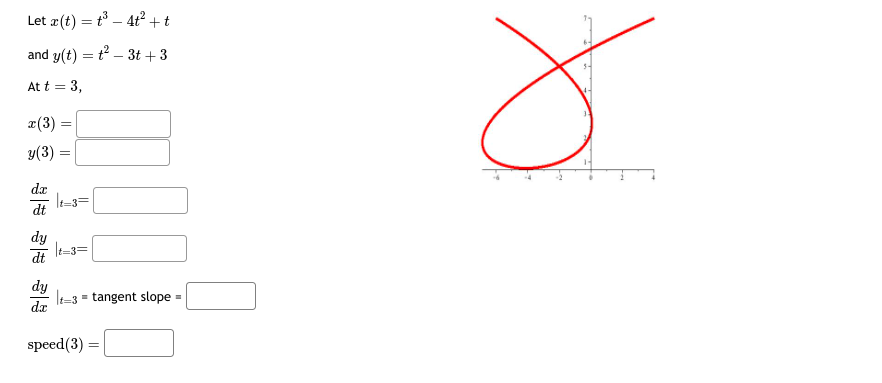
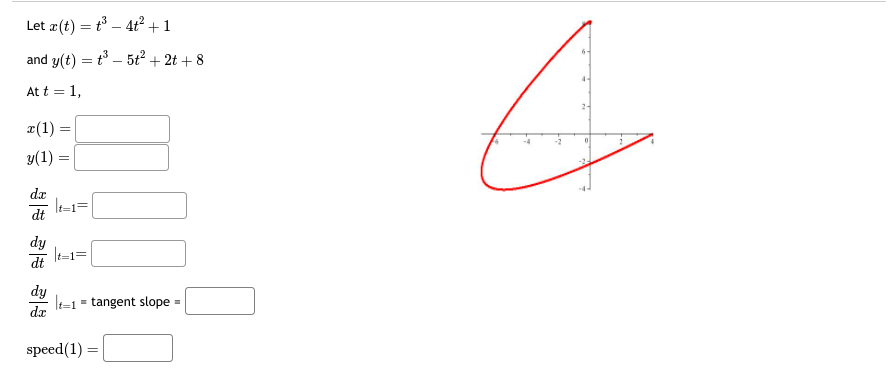
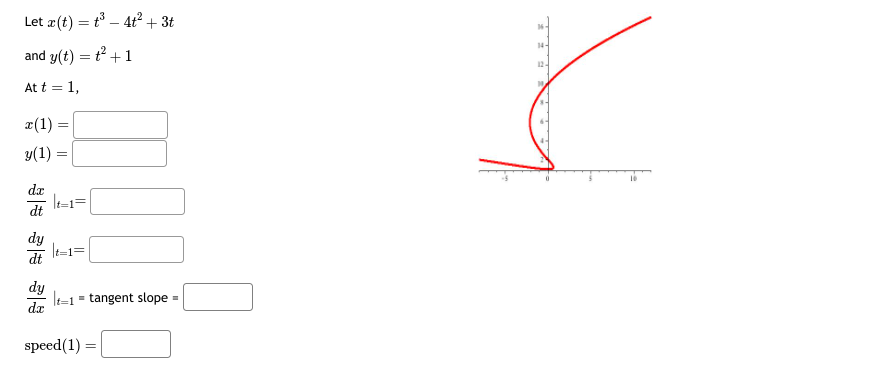
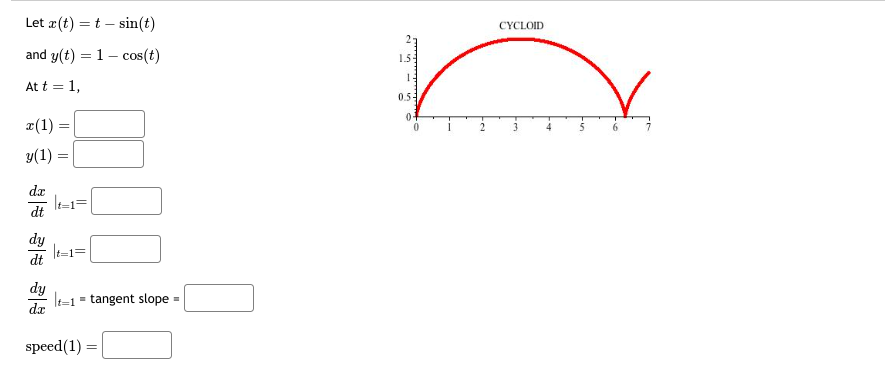
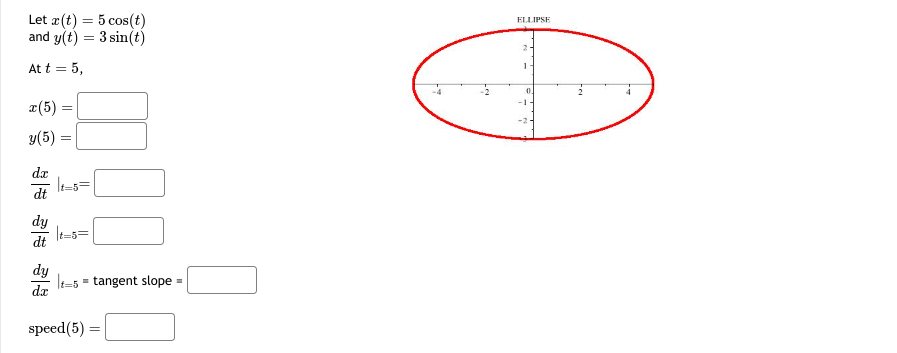
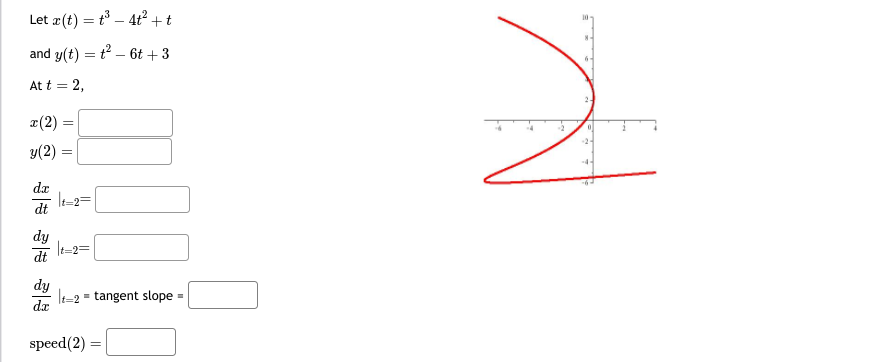
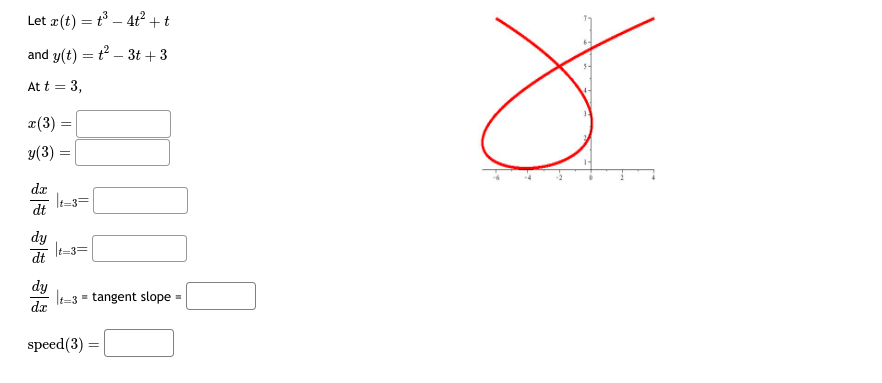
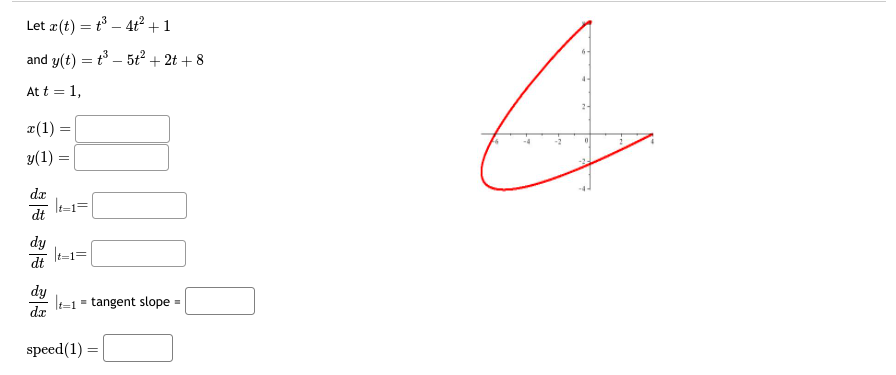
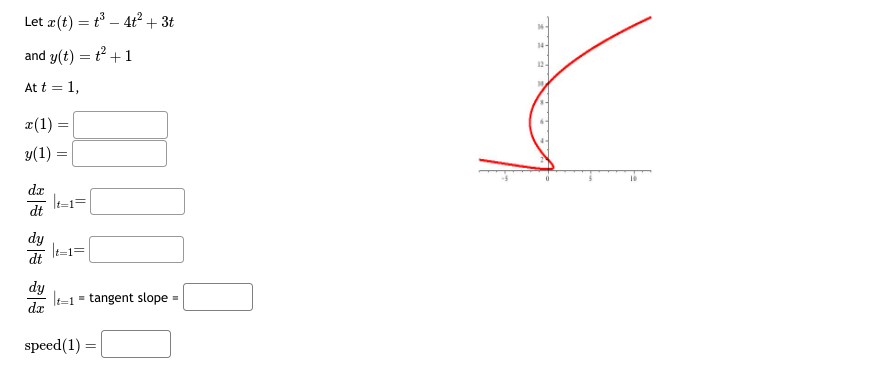
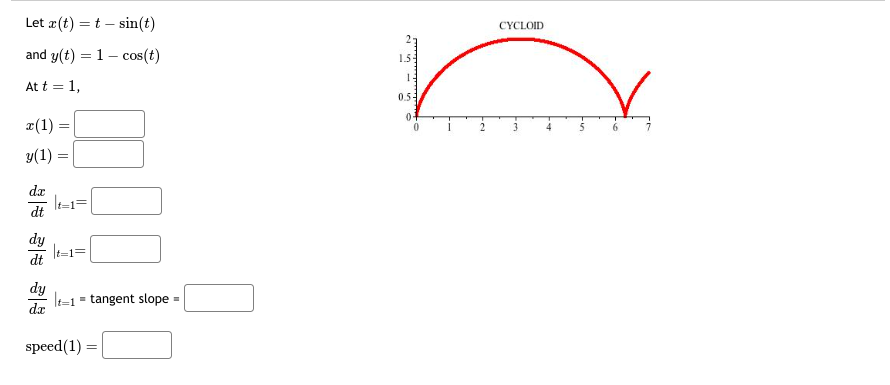
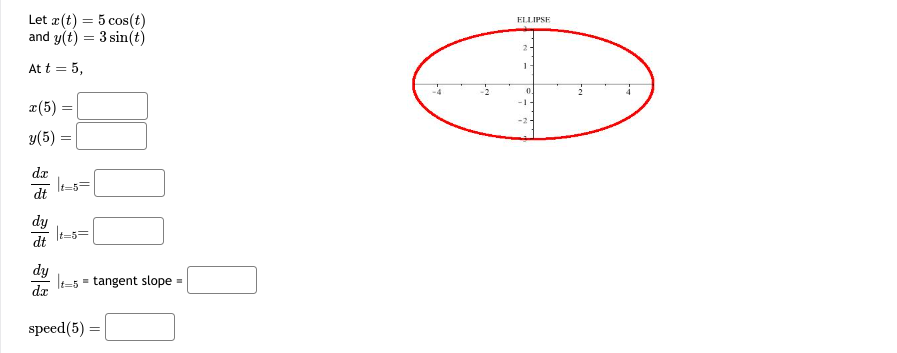
Let x(t) = t' - 4t' + 1 and y(t) = t - 5t- + 2t + 8 At t = 1, 7- (1) = y(1) -7. dt 1=1= dy dy It=1 = tangent slope = speed (1)\fLet x(t) = t - sin(t) CYCLOID and y(t) = 1 - cos(t) - At t = 1, r(1) = 2 3 5 6 7 y(1) da dt It=1= dy at =1= dy It=1 = tangent slope = speed (1) =Let x(t) = 5 cos(t) ELLIPSE and y(t) = 3 sin(t) At t = 5, T(5) = -2 y(5) = dt dy dt t=5= dy It= = tangent slope speed