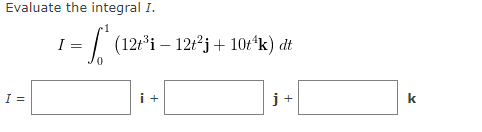
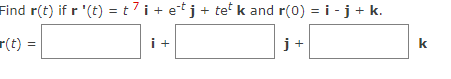
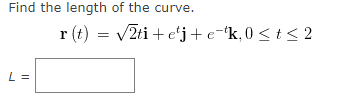
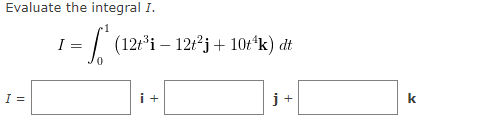
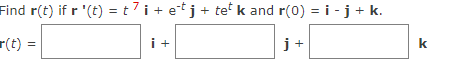
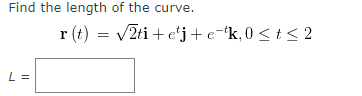
If two objects travel through space along two different curves, it's often important to know whether they will collide. (Will a missile hit its moving target? Will two aircraft collide?) The curves might intersect, but we need to know whether the objects are in the same position at the same time. Suppose the trajectories of two particles are given by the vector functions for t 2 0. Do the particles collide? If they collide find t. If not enter NONE. ri (t) = (+2, 17t - 72, t?), ra(t) = (14t - 45, +2, 16t - 63) t = NONE XEXAMPLE 3 Describe the curve defined by the vector function below. r(t) = SOLUTION The corresponding parametric equations are X = y = 2+ 5t Z = which we recognize as parametric equations of a line passing through the point (1, 2, -2) and parallel to the vector . Alternatively, we could observe that the function can be written as r = ro + tv where ro = and v = >, and this is the vector equation of a line.EXAMPLE 4 Sketch the curve whose vector equation is r(t) = 5cos(t)i + 5sin(t)j + tk SOLUTION The parametric equations for this curve are X = y = 5sin(t) Z = Since X- + V- = Video Example ()) + 25sin(t) = , the curve must lie on the circular cylinder x3 + y' = . The point (x, y, z) lies directly above the point (x, y, 0), which moves counterclockwise around the circle x2 + y' = in the xy-plane. Since z = t, the curve spirals upward around the cylinder as t increases. The curve, shown in the figure, is called a helix.Find the derivative r '(t) of the vector function r(t). r (t) = eri - j + In (1 + 3t) k r '(t) = + + kFind the unit tangent vector T(t) at the point with the given value of the parameter t. r (t) = 2vti+taj - 2tk, t = 1 T(t = 1) = i + + kThe curves r, = and ry = intersect at the origin. Find their angle of intersection, 0 correct to the nearest degree. 8 =Evaluate the integral I. = (12+31 - 12tj + 10t k) dt I = + KFind r(t) if r '(t) = t / i + elj+ tel k and r(0) = i - j + k. + k (t ) =EXAMPLE 1 Consider the function below. r(t) = (3 + #*)i + tej + sin(2t)k (a) Find the derivative. (b) Find the unit tangent vector at the point where t = 0. SOLUTION (a) We differentiate each component of r: r'(t) = i+ (1-t)e j + k (b) Since r(0) = i and r'(0) = j + 2k, the unit tangent vector at the point (3, 0, 0) is j + 2k r'(0) T(0) = Ir(0) I i + kFind the length of the curve. r V2ti+ etj + e-k,0