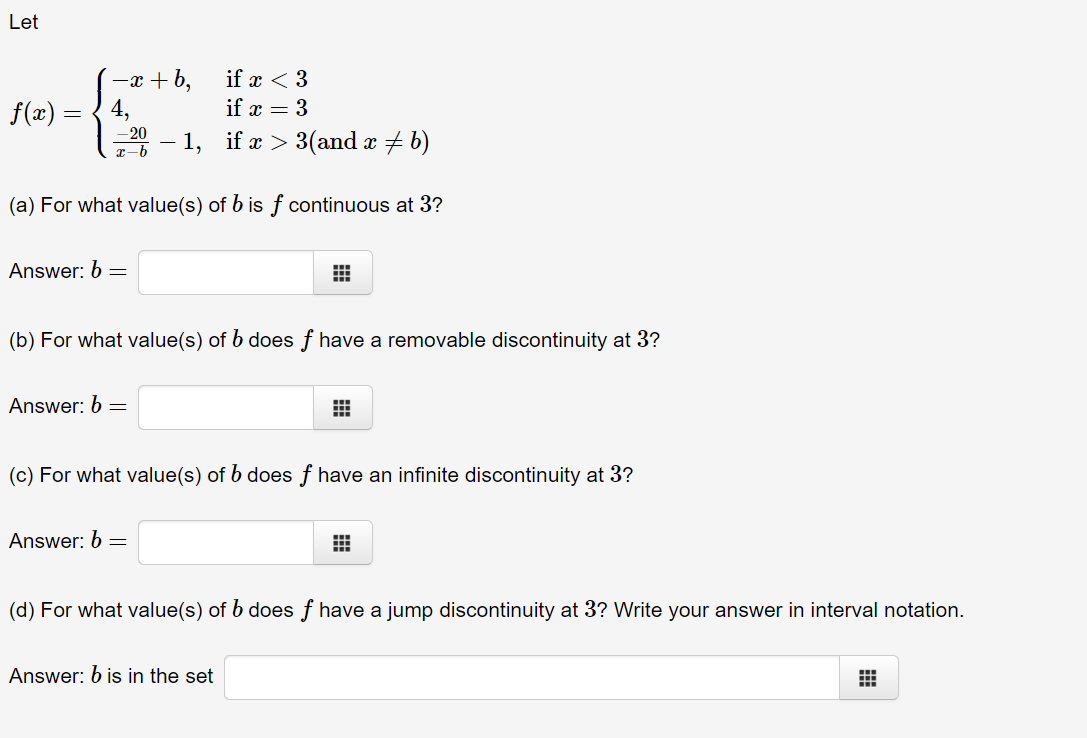
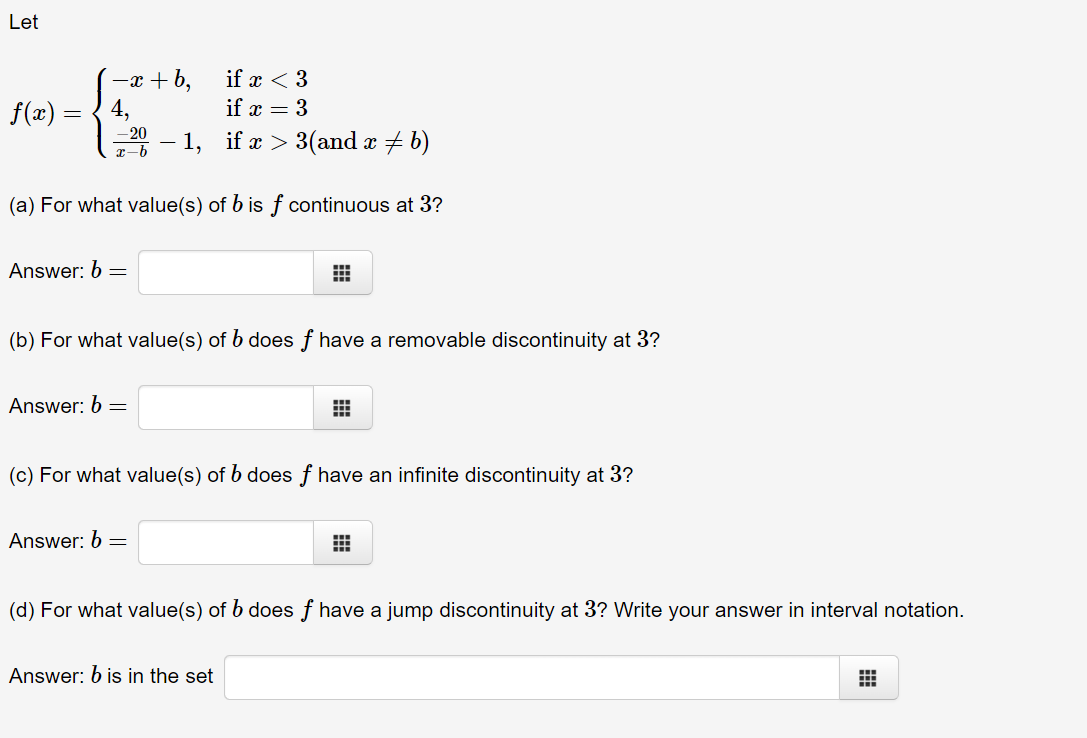
Question: Let -otb, ifx 3(and x * b) (a) For what value(s) of b is f continuous at 3? Answer: b = (b) For what value(s)


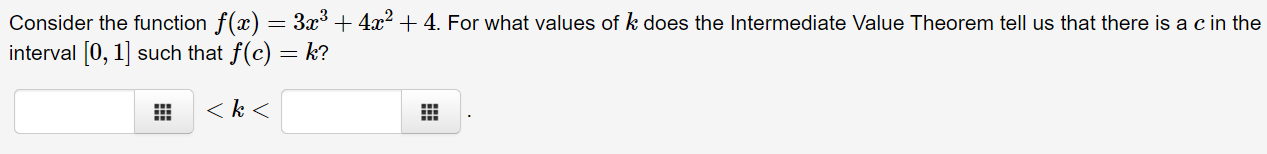

![[-2,-1] 0 [4,0] 0 [0.1] 0 [1,2] 0 None of the above](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667db933a15f4_443667db9338f129.jpg)
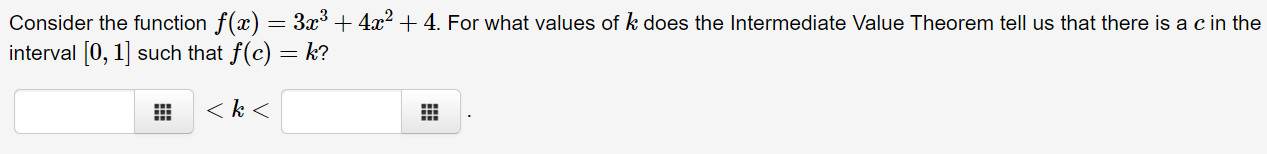
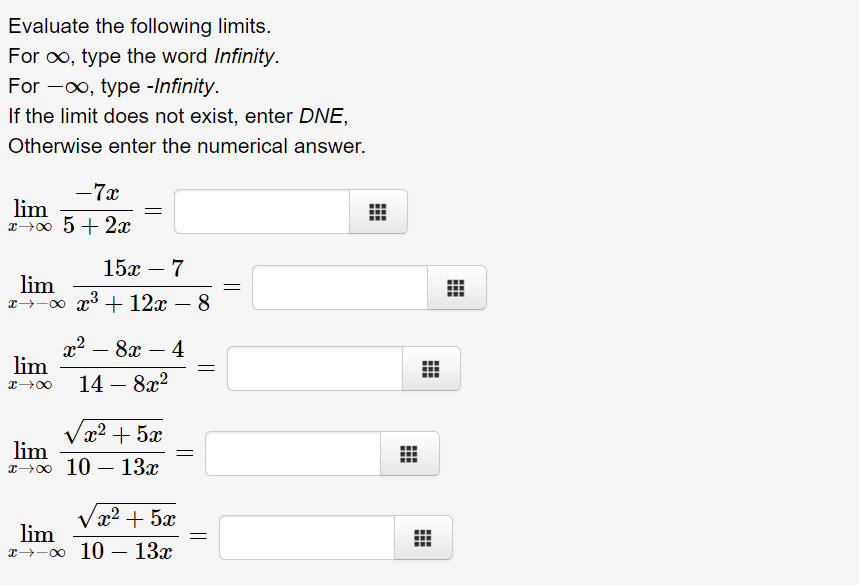
Let -otb, ifx 3(and x * b) (a) For what value(s) of b is f continuous at 3? Answer: b = (b) For what value(s) of b does f have a removable discontinuity at 3? Answer: b = (c) For what value(s) of b does f have an infinite discontinuity at 3? Answer: b = (d) For what value(s) of b does f have a jump discontinuity at 3? Write your answer in interval notation. Answer: b is in the setAccording to the Intermediate Value Theorem, which of the following intervals must contain a zero of the function f(:c) : $3 + 4:1: + 1 ? O [-2,-1] 0 [4,0] 0 [0.1] 0 [1,2] 0 None of the above Consider the function an) : 333 + 4332 + 4. For what values of It does the Intermediate Value Theorem tell us that there is a c in the interval [0, 1] such that f(c) : k? a
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


