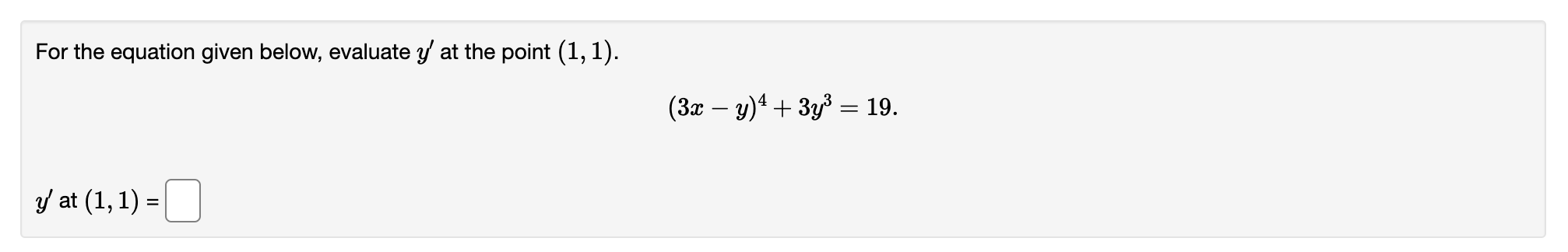
\fFor the equation given below, evaluate y' at the point (1, 1). (3x - y)4 + 393 = 19. y at (1, 1) =Use implicit differentiation to find the slope of the tangent line to the curve defined by 2wy5 + 9mg = 22 at the point (2, 1). The slope of the tangent line to the curve at the given point is C]. Find the slope of the tangent line to the curve 5 sin(m) + 2 cos(y) 3 sin(ac) cos(y) + a: = 711' at the point (77r, 71r/2). C]