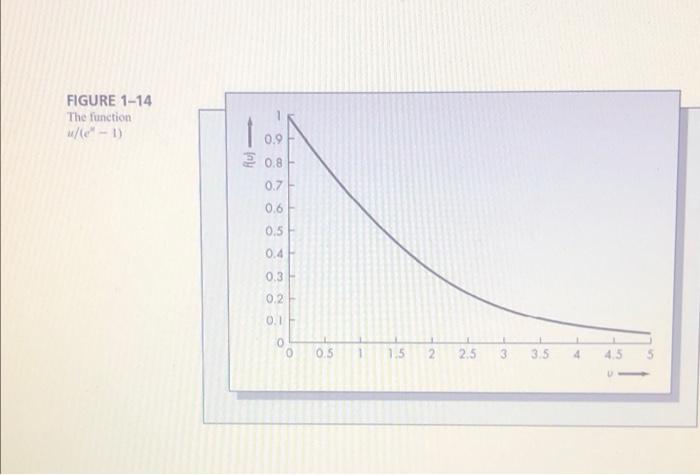
Question: (Fig 1.14 and Appendix 1-A for Problem 41 are attached to the end of this document) 41. Based on past experience, a chemicals firm estimates
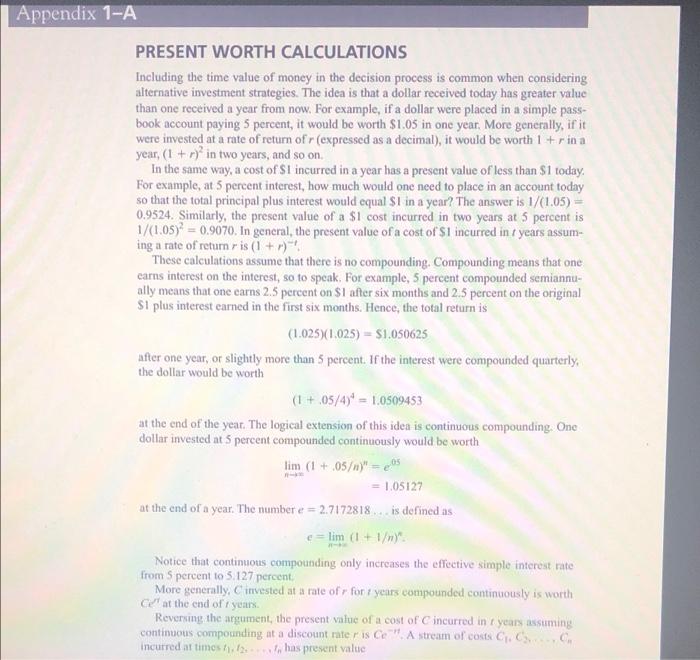
(Fig 1.14 and Appendix 1-A for Problem 41 are attached to the end of this document) 41. Based on past experience, a chemicals firm estimates that the cost of new capacity additions obeys the law [(y) = .0205.58 where y is measured in tons per year and S() in millions of dollars. Demand is growing at the rate of 3,000 tons per year, and the accounting department recom- mends a rate of 12 percent per year for discounting future costs. a. Determine the optimal timing of plant additions and the optimal size of each addition b. What is the cost of each addition? c. What is the present value of the cost of the next four additions? Assume an addition has just been made for the purposes of your calculation. (Refer to Appendix 1-A for a discussion of cost discounting.) 49. Maintenance costs for a new facility are expected to be $112,000 for the first year of operation. It is anticipated that these costs will increase at a rate of 8 percent per year. Assuming a rate of return of 10 percent, what is the present value of the stream of maintenance costs over the next 30 years? FIGURE 1-14 The function w/le-1) 0.9 ay 20.8 0.7 0.6 7.5 0.4 0.3 - 0.2 0.1 0 O 0.5 1 1.5 2 2.5 3.5 Appendix 1-A PRESENT WORTH CALCULATIONS Including the time value of money in the decision process is common when considering alternative investment strategies. The idea is that a dollar received today has greater value than one received a year from now. For example, if a dollar were placed in a simple pass- book account paying 5 percent, it would be worth $1.05 in one year. More generally, if it were invested at a rate of return of r (expressed as a decimal), it would be worth 1 +rina year, (1 + r) in two years, and so on. In the same way, a cost of SI incurred in a year has a present value of less than $1 today. For example, at 5 percent interest, how much would one need to place in an account today so that the total principal plus interest would equal $1 in a year? The answer is 1/(1.05) - 0.9524. Similarly, the present value of a $1 cost incurred in two years at 5 percent is 1/(1.05) = 0.9070, In general, the present value of a cost of Si incurred in / years assum- ing a rate of returnris (+7) These calculations assume that there is no compounding. Compounding means that one carns interest on the interest, so to speak. For example, 5 percent compounded semiannu- ally means that one carns 2.5 percent on $1 after six months and 2.5 percent on the original SI plus interest camned in the first six months. Hence, the total return is (1.025)1.025) = $1.050625 after one year, or slightly more than 5 percent. If the interest were compounded quarterly, the dollar would be worth (1 + 05/4) * = 1.0509453 at the end of the year. The logical extension of this idea is continuous compounding. One dollar invested at 5 percent compounded continuously would be worth lim (1 + 05)" 205 = 1.05127 at the end of a year. The number e = 2.7172818 is defined as e = lim (1 + 1 Notice that continuous compounding only increases the effective simple interest rate from 5 percent to 5.127 percent More generally, invested at a rate of r for years compounded continuously is worth C' at the end of r years Reversing the argument, the present value of a cost of Cincurred in r years assuming continuous compounding at a discount rater is Ce. A stream of costs C..., incurred at times) has present value 1 after one year, or slightly more than 5 percent. If the interest were compounded quarterly, the dollar would be worth (1 +.05/4)* = 1.0509453 at the end of the year. The logical extension of this idea is continuous compounding. One dollar invested at 5 percent compounded continuously would be worth lim (1 +.05)" = 0,05 1.05127 at the end of a year. The number e = 2.7172818.. is defined as + e = lim (1 + 1)" Notice that continuous compounding only increases the effective simple interest rate from 5 percent to 5.127 percent. More generally, C invested at a rate of r for 7 years compounded continuously is worth Cet at the end of t years. Reversing the argument, the present value of a cost of Cincurred in t years assuming continuous compounding at a discount rate ris CeA stream of costs C. C2...., CH incurred at times ti, 12,..., has present value cer A comprehensive treatment of discounting and its relationship to the capacity expansion problem can be found in Freidenfelds (1981)