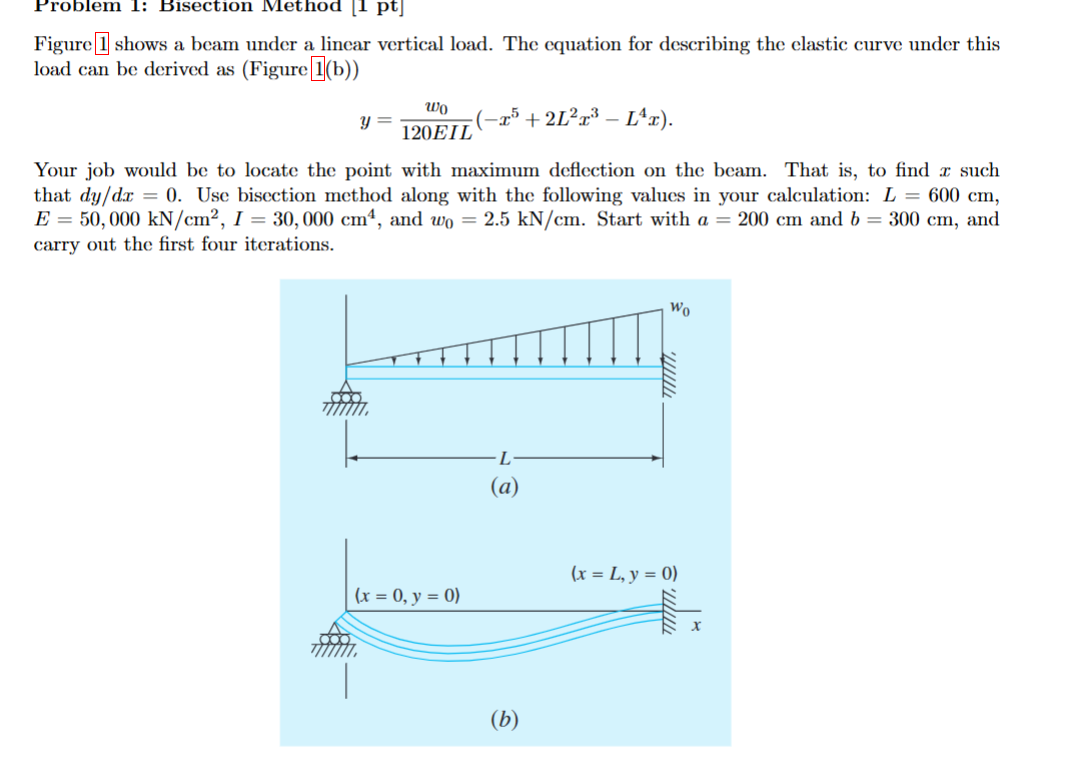
Figure $1$ shows a beam under a linear vertical load. The equation for describing the elastic curve under this Problem $1$: Bisection Method $[1$ pt$]$

Figure $1$ shows a beam under a linear vertical load. The equation for describing the elastic curve under this load can be derived as $($Figure $1($b$))$

$y=\frac{w_0}{120\text{E}\text{I}\text{L}}(-x^5+2L^2{x}^3-L^{4}x)$

Your job would be to locate the point with maximum deflection on the beam. That is$,$ to find $x$ such that $d\frac{y}{d}x=0.$ Use bisection method along with the following values in your calculation: $L=600cm,E=50,000k\frac{N}{c}{m}^2,I=30,000c{m}^4,$ and $w_0=2\mathrm{.}5k\frac{N}{c}m.$ Start with $a=200cm$ and $b=300cm,$ and carry out the first four iterations.

load can be derived as $($Figure $1($b$))$

y $=$ w$0$

$120$EIL $($x$5+2$L$2$x$3$ L$4$x$).$

Your job would be to locate the point with maximum deflection on the beam. That is$,$ to find x such

that dy$/$dx $=0.$ Use bisection method along with the following values in your calculation: L $=600$ cm$,$

E $=50,000$ kN$/$cm$2,$ I $=30,000$ cm$4,$ and w$0=2\mathrm{.}5$ kN$/$cm$.$ Start with a $=200$ cm and b $=300$ cm$,$ and

carry out the first four iterations.PROBLEMS

computation: L $=600$ cm$,$ E $=50,000$ kN$/$cm$2$

$,$ I $=$

$30,000$ cm$4$

$,$ and w$0=2\mathrm{.}5$ kN$/$cm$.$

$5\mathrm{.}14$ You buy a $$35,000$ vehicle for nothing down at $$8,500$

per year for $7$ years. Use the bisect function from Fig. $5\mathrm{.}7$

to determine the interest rate that you are paying. Employ

initial guesses for the interest rate of $0\mathrm{.}01$ and $0\mathrm{.}3$ and a stop$-$

ping criterion of $0\mathrm{.}00005.$ The formula relating present

worth P$,$ annual payments A$,$ number of years n$,$ and interest

rate i is

A $=$ P i$(1+$ i$)$n

$5\mathrm{.}16$ The resistivity $\backslash$rho of doped si

charge q on an electron, the electron

tron mobility $\backslash$mu $.$ The electron densit

the doping density N and the intrinsic

electron mobility is described by the

erence temperature T$0,$ and the refer

equations required to compute the res

$\backslash$rho $=1$

qn$\backslash$mu

where

n $=1$

$2$

$($

N $+$

$$

N $2+4$n$2$

i

$)$

and

Determine N$,$ given T$0=300$ K$,$

$1360$ cm $2($V s$)1,$ q $=1\mathrm{.}7\backslash$times $1019$ C

and a desired $\backslash$rho $=6\mathrm{.}5\backslash$times $106$ V s

guesses of N $=0$ and $2\mathrm{.}5\backslash$times $1010.$

$($b$)$ the false position method.

$5\mathrm{.}17$ A total charge Q is uniformly di

shaped conductor with radius a$.$ A c

distance x from the center of the ring

exerted on the charge by the ring is g

F $=1$

$4\backslash$pi e$0$

q Qx

$($x$2+$ a$2)3/2$

where e$0=8\mathrm{.}9\backslash$times $1012$ C $2$

$/($N m$2$

$).$ Fi

the force is $1\mathrm{.}25$ N if q and Q are $2\backslash$times

radius of $0\mathrm{.}85$ m$.$

$5\mathrm{.}18$ For fluid flow in pipes, friction

mensionless number, the Fanning fri

ning friction factor is dependent on a

related to the size of the pipe and

all be represented by another dime

Reynolds number Re$.$ A formula tha

w$0$

L

$($a$)$

$($x $=0,$ y $=0)$

$($x $=$ L$,$ y $=0)$

x

$($b$)$

FIGURE P$5\mathrm{.}13$

cha$01102\_$ch$05\_123-150.$qxd $12/17/108$:$01$ AM Page $149$

Figure $1$: Beam deflection problem.

Problem $2$: False Position Method $[1$ pt$]$

Determine the positive roots of the equation cos$($x$)0\mathrm{.}8$x$2=0$ by using the false position method. Carry

out the first five iterations. Start with a $=0\mathrm{.}5$ and b $=1\mathrm{.}5.$

$1$