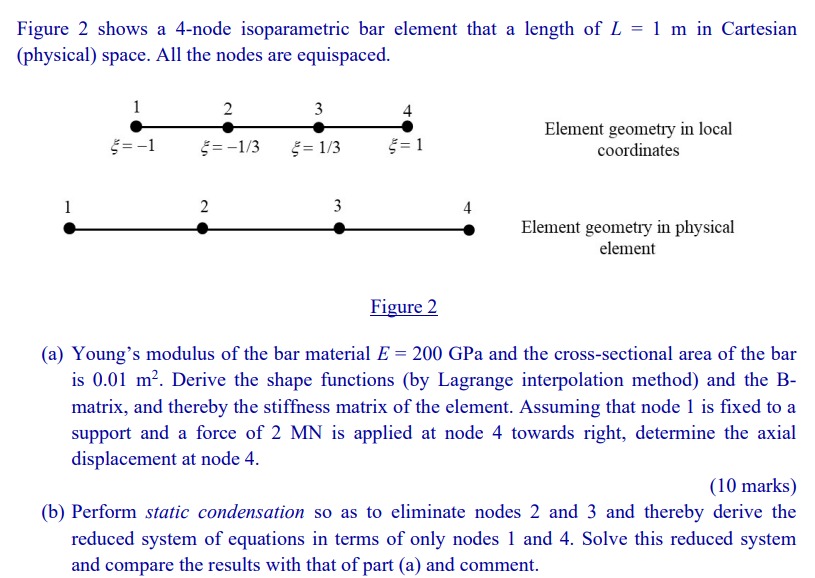
Figure $2$ shows a $4-$node isoparametric bar element that a length of $\backslash ($ L$=1\backslash$mathrm$\{$~m$\}\backslash )$ in Cartesian $($physical$)$ space. All the nodes are equispaced.

Element geometry in local coordinates

Element geometry in physical element

Figure $2$

$($a$)$ Young's modulus of the bar material $\backslash ($ E$=200\backslash$mathrm$\{$GPa$\}\backslash )$ and the cross$-$sectional area of the bar is $\backslash (0\mathrm{.}01\backslash$mathrm$\{$~m$\}^\{2\}\backslash ).$ Derive the shape functions $($by Lagrange interpolation method$)$ and the Bmatrix, and thereby the stiffness matrix of the element. Assuming that node $1$ is fixed to a support and a force of $2$ MN is applied at node $4$ towards right, determine the axial displacement at node $4.$

$(10$ marks$)$

$($b$)$ Perform static condensation so as to eliminate nodes $2$ and $3$ and thereby derive the reduced system of equations in terms of only nodes $1$ and $4.$ Solve this reduced system and compare the results with that of part $($a$)$ and comment.