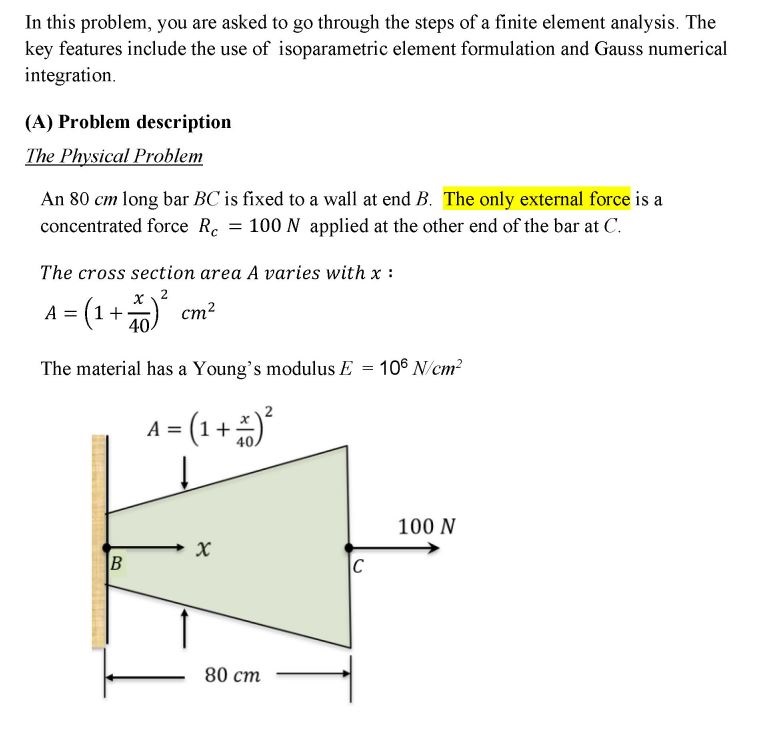
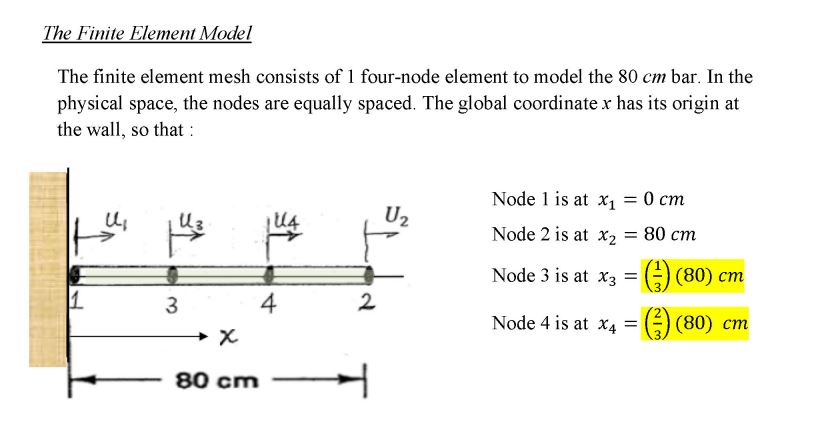
In this problem, you are asked to go through the steps of a finite element analysis. The key features include the use of isoparametric element formulation and Gauss numerical integration. (A) Problem description The Physical Problem An 80 cm long bar BC is fixed to a wall at end B. The only external force is a concentrated force Rc = 100 N applied at the other end of the bar at C. The cross section area A varies with x : 2 A = (1++) cm 40 The material has a Young's modulus E = 106 N/cm 1=(1+1) = (1 + x) B X 80 cm C 100 N The Finite Element Model The finite element mesh consists of 1 four-node element to model the 80 cm bar. In the physical space, the nodes are equally spaced. The global coordinate x has its origin at the wall, so that : Node 1 is at x1 = 0 cm U2 Node 2 is at x2 = 80 cm Node 3 is at x3 = () = () (80) cm 3 4 2 Node 4 is at x4 = = () (80) cm 80 cm Isoparametric Finite Element Formulation The four-node element modeling the 80-cm long bar in the physical space (the x- coordinate) is mapped into the following isoparametric element in the r-coordinate space (natural coordinate or isoparametric coordinate space). It has a length of 2, and the origin of the r-coordinate is at the center of the element, as shown. U4 U2 Node 1 is at r = -1 Node 2 is at r2 = +1 >r Node 1 3 4 2 Node 3 is at r3 = Node 4 is at 14 = () 11-113 1 13 14 113 1. 12=1 (B) Deliverables for this problem: You are asked to proceed step-by-step consistent with the isoparametric finite element formulation and Gauss numerical integration. (1) Determine the displacement interpolation function matrix H(r) of the element. (2) Determine the Jacobian matrix J, and det J, of this element. (3) Determine the strain-displacement matrix B(r) of the element. (4) Use Gauss numerical integration to determine the element stiffness matrices K(1) of element 1. (For this cubic element, use Gauss numerical integration with 4 sampling points in r). (5) Assemble the global stiffness matrix K. Since we have only 1 element, the global stiffness matrix K = K() (6) Determine the global load vector R (7) Impose the boundary condition U = 0 on the global equation KU = R and solve for the nodal displacements. (8) Post-processing: With the nodal displacements (U1, U2, U3, U4) solved, perform postprocessing: (a) Generate a plot showing displacement u(x) versus x along the length of the bar, from x=0 cm to x= 80 cm (b) Generate another plot showing the stress (x) versus x along the length of the bar, from x=0 cm to x= 80 cm. (c) On the same plot of u(x) in part (a) above, add the following: Plot the exact solution of the displacement u(x) vs x, (d) On the same plot of (x) in part (b) above, add the following: Plot the exact solution of the stress (x) vs x. (e) Use a table to list the values of the displacement u and stress at the nodes, (Show 6 significant digits, e. g., 0.000122301, 1.22301 10-4, or 1.22301E 4.) At Node-1 At Node-2 At Node-3 At Node-4 Displacement, u Stress, Hint: This problem has an exact solution. After we obtain the approximate solution using the fintie element method, we can compare the approximate solution with the exact solution. The exact solution for the stress at any point x, (x), can be deermined by force balance on the following free body diagram (created by cutting the bar at x): (x). A(x) C x 80 cm Rc = 100 N (x). A(x) = Rc (x). A(x) = 100 N 100 N So, (x) = A(x) 100 N [olexact 2 x 1 + cm 40, The strain at any point x, (x), is given by E(x) = (x) 100 So, (x): = E.A(x) du Since = dx strain: the exact solution for displacement u(x) can be obtained by integrating the du > du = dx dx u(x) = f (x)dx = . So x 100 E.A(x) dx = . =So- x 100 dx. E.(1+)