Question: Let f, define the Fibonacci numbers, where fo = 0, f = 1, and fn+2= fn+1+fn for all n > 0. Let P (n)

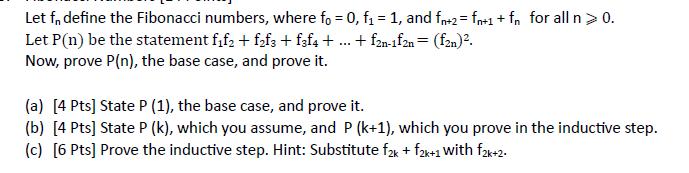
Let f, define the Fibonacci numbers, where fo = 0, f =

Let f, define the Fibonacci numbers, where fo = 0, f = 1, and fn+2= fn+1+fn for all n > 0. Let P (n) be the statement ff +ff3 + f3f4 + + f2n-1f2n = (f2n). Now, prove P(n), the base case, and prove it. (a) [4 Pts] State P (1), the base case, and prove it. (b) [4 Pts] State P (k), which you assume, and P (k+1), which you prove in the inductive step. (c) [6 Pts] Prove the inductive step. Hint: Substitute f2k + f2k+1 with f2k+2.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Frbonacci Number series proof Base case pa f f f Q ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

Find and describe a "strategic principle" for an organization not already presented in the article Transforming Corner-Office Strategy into Frontline Action.

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

A compare-exchange operation on two array elements A[i] and A[j], where i A[j] 2 exchange A[i] with A[j] After the compare-exchange operation,...

DEFINE TABLE AUTHORS WITH COLUMNS AUTHORID INT AND AUTHORNAME VARCHAR(30),ADD COLUMN LEVEL PRIMARY KEY CONSTRAINT FOR AUTHORID, ADD COLUMN LEVEL NOT NULL CONSTRAINT FOR AUTHORNAME 2. DEFINE TABLE...

A diatomic molecule is found to have an activation energy of 1.3 eV. When the molecule is disassociated, 1.6 eV of energy is released. Draw a potential energy curve for this molecule.

The trial balance of Fugazy Investment Advisers at December 31, 2012, follows: Adjustment data at December 31, 2012: a. Unearned service revenue earned during the year, $500. b. Supplies on hand,...

What is a dummy variable?

Jain Simmons Company needs 10,000 units of a certain part to be used in production. If Jain Simmons buys the part from Sullivan Company instead of making it themselves, Jain Simmons could not use the...

A new accountant at Marin Inc. is trying to identify which of the amounts shown below should be reported as the current asset "Cash and cash equivalents" in the year-end balance sheet, as of April...

With respect to the Ethernet frame: a . Show the frame format including the name, size ( in decimal ) , and the content ( in Hex ) of each field ( do not convert content to decimal or binary ) . ...

An SKU costing $20 is ordered in quantities of 800 units, annual demands is 12,000 units, carrying costs are 15% of average inventory size, and the cost of placing an order is $100. Calculate the...

Case Study: The mobile phone industry The mobile phone industry case is contained in the two Economist articles, "Battling for the palm of your hand" and "Upwardly mobile". Link:...

Jack and Jill recently negotiated a rate of 2% on their mortgage loan that has a 5-year term and 25-year amortization period. The Bank of Canada 5-year benchmark mortgage rate is 4.8%. What would be...

Question 15 Which premise doesn't address accident prevention? Accidents are always human error. O Accidents have causes. Accidents involve hazards that lead to unsafe acts and conditions. Accidents...

When analyzing the poetry of Marianne Moore, Donald Hall claims that in her view, "The raw material for poetry abounds, it is everywhere, is anything." How does the poetry of Moore and Plath express...

An imaginary object moves horizontally. The position-versus-time function represents the object's motion mathematically. Work together with your group, and when you're done or if you get stuck,...

On May 20, the board of directors for Auction.com declared a cash dividend of 50 cents per share payable to stockholders of record on June 14. The dividends are paid on July 14. The company has...

Experiment: Tossing four coins Event: Getting three heads Identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when...

The use- case diagram is an important part of UML diagramming. Use the Web search engines to learn about the use cases diagram. Prepare a use- cases diagram for the following situation. A bank...

In a large manufacturing organization supplying goods and services, several departments may be involved in the processing of customer complaints and the issuance of any resulting credit memos....

Discuss the advantages and disadvantages of having an industry- wide standard to which all database software systems conform.

Why do workers sometimes resent time studies?

If an average worker could be identified, what advantage would there be in using that person for a stopwatch time study? What are some reasons an average worker might not be studied?

What are tire key advantages and disadvantages of: a. Time-based pay? (i) for management and (ii) workers? b. Piece rate (output-based) pay? (i) for management and (ii) workers?