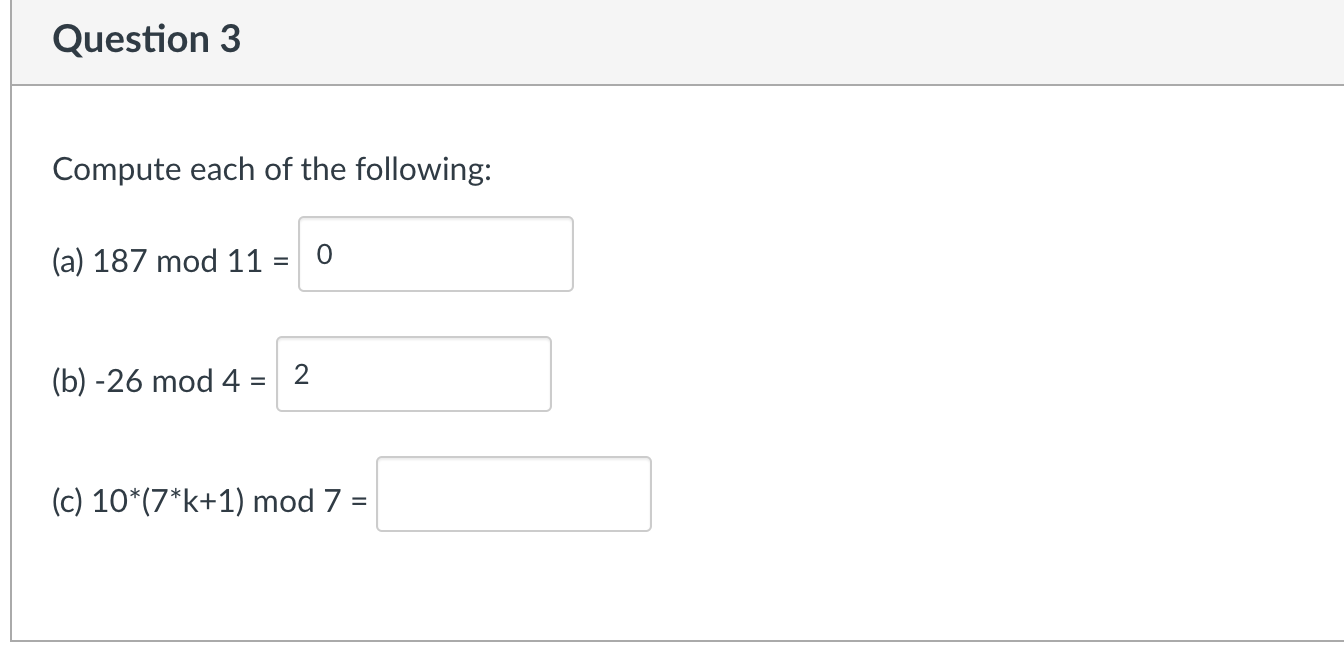
Fill in the missing steps in the following formal proof. Please note, in Canvas answers you must use "A" to indicate a power, as in "n^2" to mean "n2". Proposition: Every odd perfect square can be written in the form 4k+1, where k is an integer. Proof: Let s be an odd perfect square. So, s = n^2 for some integer n, and n^2 is odd. By contrapositive to the solution to Section 2.1, Problem 5(b), if n^2 is odd, then n is odd. Since n is odd, there is an integer L such that n = This means that s = n^2= ( 4k+1 1)^2= So, s = 4( ) + 1, where is an integer, as desired. Question 3 Compute each of the following: (a) 187 mod 11 = 0 (b) -26 mod 4 = 2 (c) 10*(7*k+1) mod 7 =