Final Practice T1 Q5 - Looking for a detailed worked solution with theoretical explanation

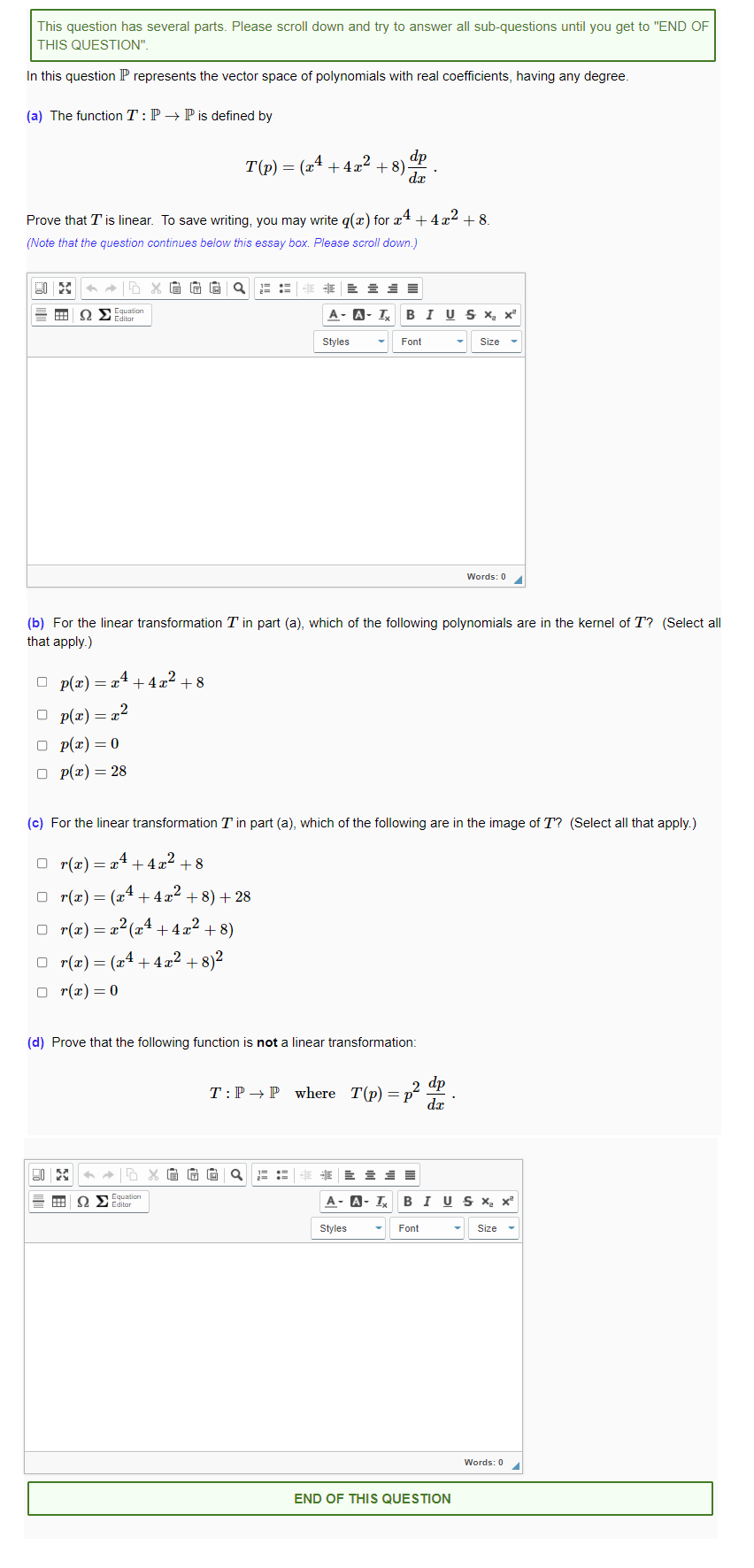
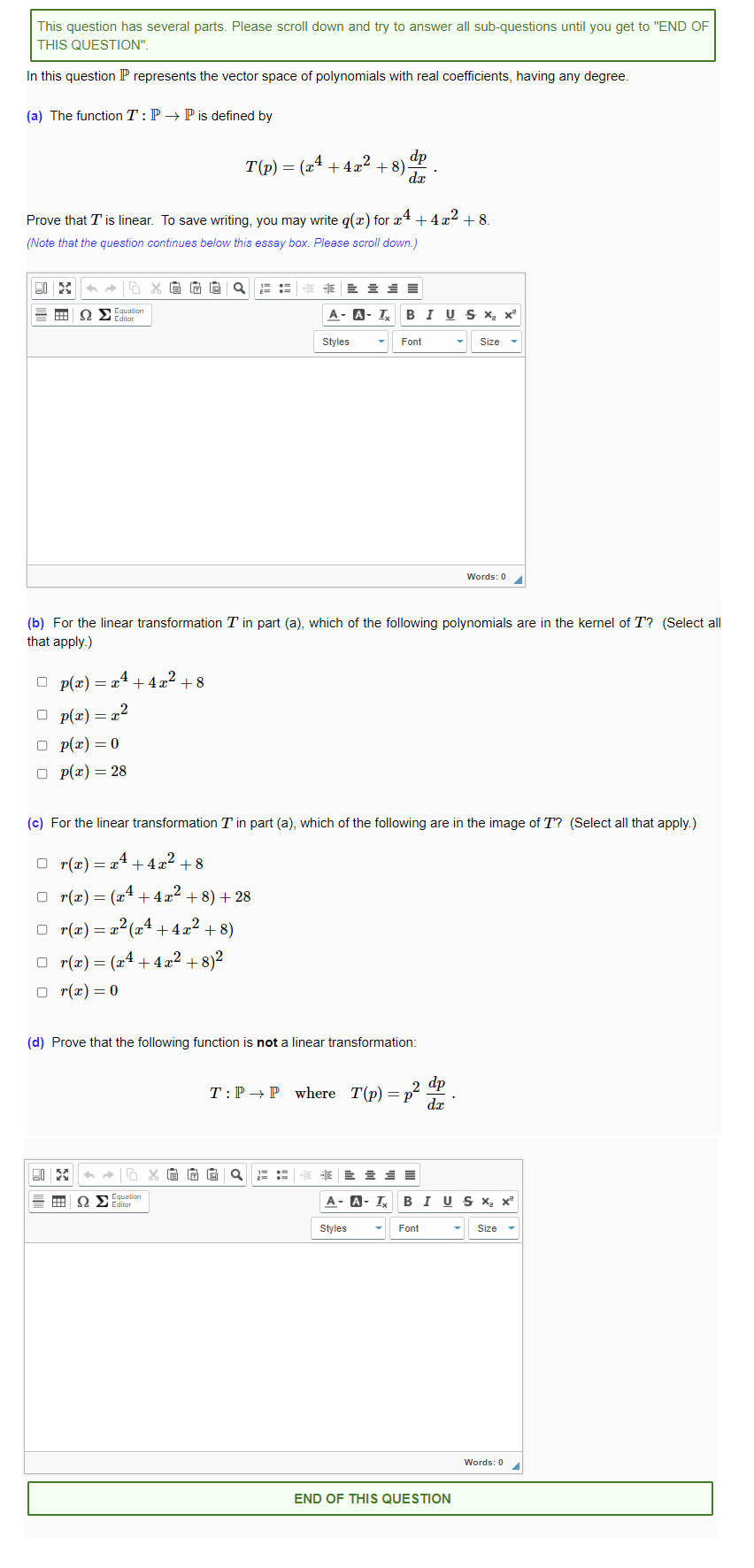
This question has several parts. Please scroll down and try to answer all sub-questions until you get to "END OF THIS QUESTION". In this question IP represents the vector space of polynomials with real coefficients, having any degree. (a) The function T : P - P is defined by T(p) = (24+4x2 +8) d. dp Prove that T' is linear. To save writing, you may write q(x) for x 4 + 4x2 + 8. (Note that the question continues below this essay box. Please scroll down.) Q Equation A- A-IX BIUSX X Styles Font Size Words: 0 (b) For the linear transformation T' in part (a), which of the following polynomials are in the kernel of T? (Select all that apply.) O p(x) =24+412+8 O p(x) = x2 O P(x) =0 O P(x) =28 (c) For the linear transformation T in part (a), which of the following are in the image of T? (Select all that apply.) Or(x) =14+4x2+8 or(x) = (24+412+8)+28 or(x) =12(24+412+8) O r(x) = (24+412 +8)2 Or(x) =0 (d) Prove that the following function is not a linear transformation: T : P-P where T(P) = P dx 2 dp Q > Editor A- A-Ix BIUSX X Styles Font Size Words: 0 END OF THIS