Question: Financial Mathematics Let e be a given integrable function. For each (t, s) E R define B(t, s) = exp E(T) dT. Show that the

Financial Mathematics

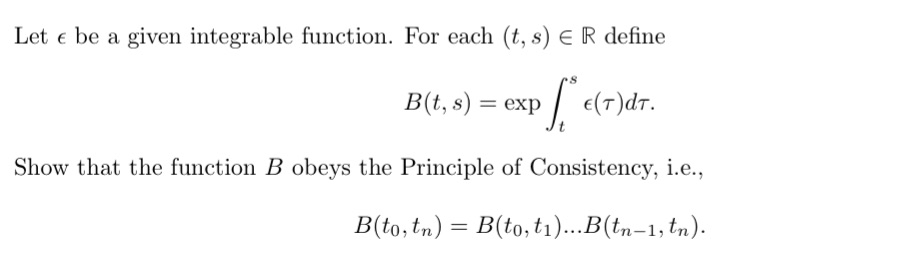
Let e be a given integrable function. For each (t, s) E R define B(t, s) = exp E(T) dT. Show that the function B obeys the Principle of Consistency, i.e., B(to, tn) = B(to, t1)...B(tn-1, tn)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Part 1: Let e be a given integrable function. For each (t, s) R define p (fe(7)dr). Show that the function B obeys the Principle of Consistency, i.e., B(to, tn)= B(to, t)...B(tn-1, tn). B(t, s) = exp...

E-Physics Tutorial Book Note: I have attached below the lesson for the 3 activities. Thank you so much for your time and effort. Activity 1. Directions: Use the right-hand rule to determine the...

re Regular Languages and Finite Automata (a) Let L be the set of all strings over the alphabet {a, b} that end in a and do not contain the substring bb. Describe a deterministic finite automaton...

(i) Write down the linear program relaxation for the vertex cover problem and solve the linear program. [6 marks] (ii) Based on the solution of the linear program in (b)(i), derive an integer...

hen we contrive an assumption that the existence of primitive recursive functions pair N 2 N, fst N N and snd N N satisfying for all x, y N fst(pair (x, y)) = x snd(pair (x, y)) = y prove by...

"There is a growing interdependence between a firm's ability to use information technology and its ability to implement corporate strategies and achieve corporate goals." "To fully understand...

please provide steps 5. a. Let K, T, o and r be positive constants, and define the function g : R - R as "b(z ) g(2) - VZx Jo e - z dy where box) = ( In (#) + (r+ 2 ) T) / (GVT ). Compute g'(x)....

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

8.1. Dulles Electric Company buys 1 million tons of coal annually to burn at its power plant. The company wants to invest in a unit train that will haul coal from the mine to the power house, where...

6.1. Carbondale Company has the following credit policy 2/10, net 30. Carbondale also charges 1% per month interest on all accounts after 30 days. The following table shows the collection schedule of...

Briefly describe the two primary qualities of useful accounting information.

Happy Snacks Ltd. (HSL) is a distributor of snack products to various retail stores in Toronto. HSL establishes agreements with stores whereby it places racks in the stores that display HSL's...

Which of the following statements is true? Multiple Choice Pellagra is the vitamin D deficiency disorder in adults. Skin can form previtamin D after being exposed to sunlight. Vitamin D is necessary...

2023 1040 form 1.Phillip and Claire are married and file a joint return. Phillip is self-employed as a real estate agent, and Claire is a flight attendant. Phillip and Claire have three dependent...