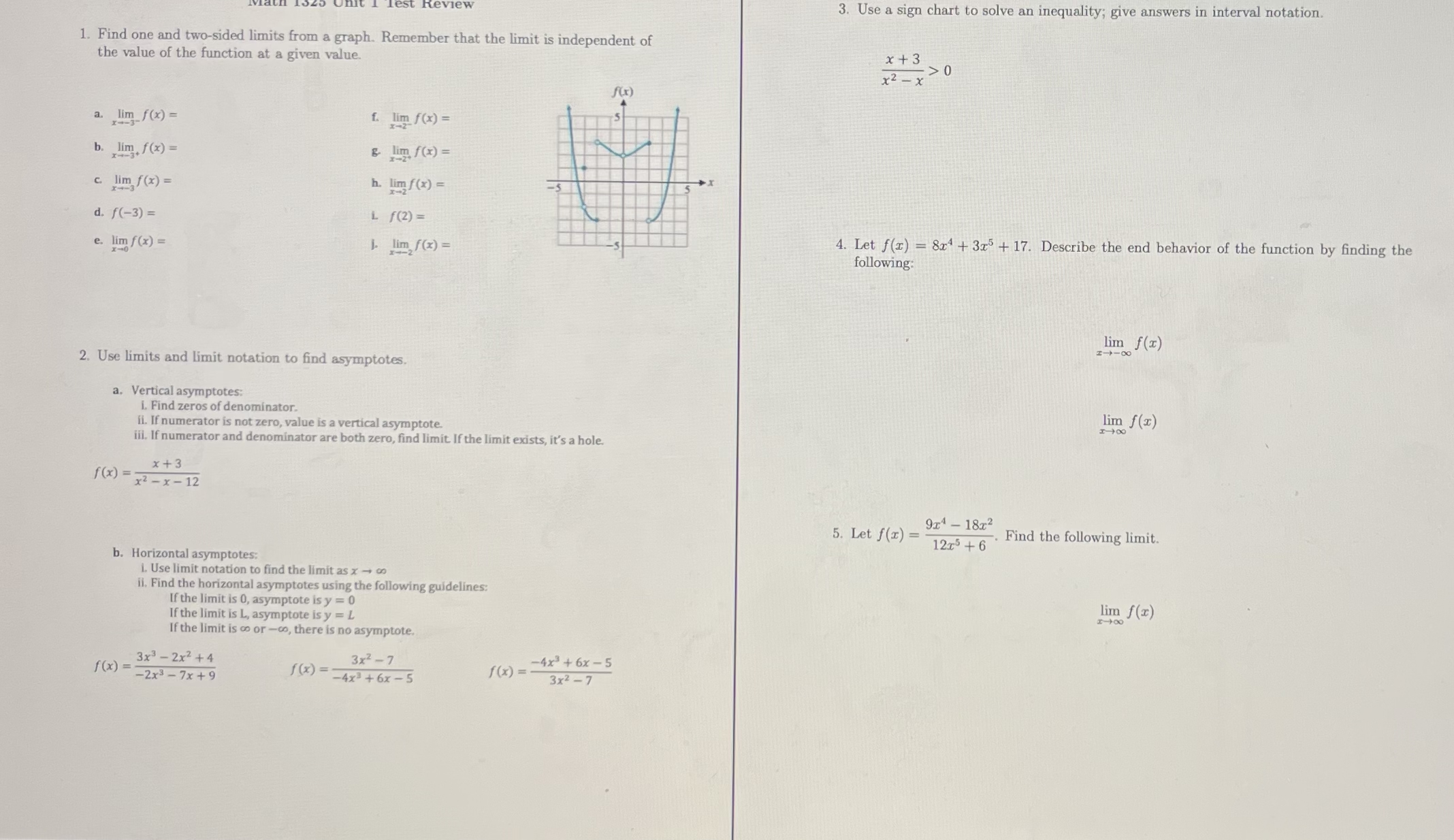
Question: Find one and two - sided limits from a graph. Remember that the limit is independent of the value of the function at a given
Find one and twosided limits from a graph. Remember that the limit is independent of the value of the function at a given value.
a
f
b
c
g
h
d
e
Use limits and limit notation to find asymptotes.
a Vertical asymptotes:
i Find zeros of denominator.
ii If numerator is not zero, value is a vertical asymptote.
iii. If numerator and denominator are both zero, find limit If the limit exists, it's a hole.
b Horizontal asymptotes:
Use limit notation to find the limit as
ii Find the horizontal asymptotes using the following guidelines:
If the limit is asymptote is
If the limit is asymptote is
If the limit is or there is no asymptote.
Use a sign chart to solve an inequality; give answers in interval notation.
Let Describe the end behavior of the function by finding the following:
Let Find the following limit
Use correct notation to outline the fourstep process and use the process to find the derivative of a quadratic function.
Use differentiation rules, including rules for negative and fractional exponents. Be clear about notation; use and accurately.
a
b
c
Apply the derivative to tangent lines; find the slope of a tangent line, the equation for a tangent line, and the values where the tangent line is horizontal.
Let
a Find
b Find the slope of the graph of at
c Find the equation of the tangent line at
d Find the values of where the tangent line is horizontal.
Interpret values of a function and its derivative involving rate of change. Units on the derivative are always rates: per
The total sales in millions of dollars months from now will be given by
Find and and interpret the results.
Use pricedemand functions to find revenue and marginal revenue. Interpret results.
The price p in dollars and the demand x for a particular steam iron are related by the equation
a Express the price in terms of the demand
b Find the revenue from the sale of
c Find the marginal revenue at a production level of steam irons and interpret the results.The total cost in dollars of producing food processors is
a Find the exact cost of producing the st food processor.
b Use marginal cost to approximate the cost of producing the st food processor.
Find average and marginal profit functions. Interpret results at a specific value.
The profit from sales of lawn mowers is given by
a Find
b Find
c Find and interpret the results.
d Find and interpret the results.
e Find and interpret the results.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


