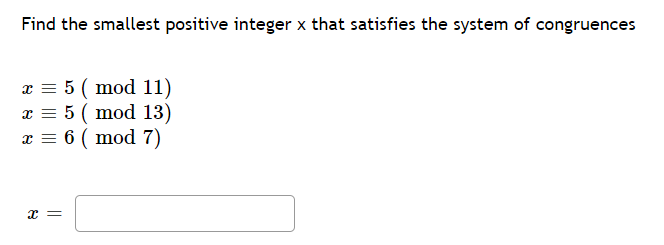
Question: Find the smallest positive integer x that satisfies the system of congruences 325(m0d11) m25(m0d13) 326(m0d7) Pl Find the smallest positive inverse of 71 modulo 1000.Find



Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


