please answer these

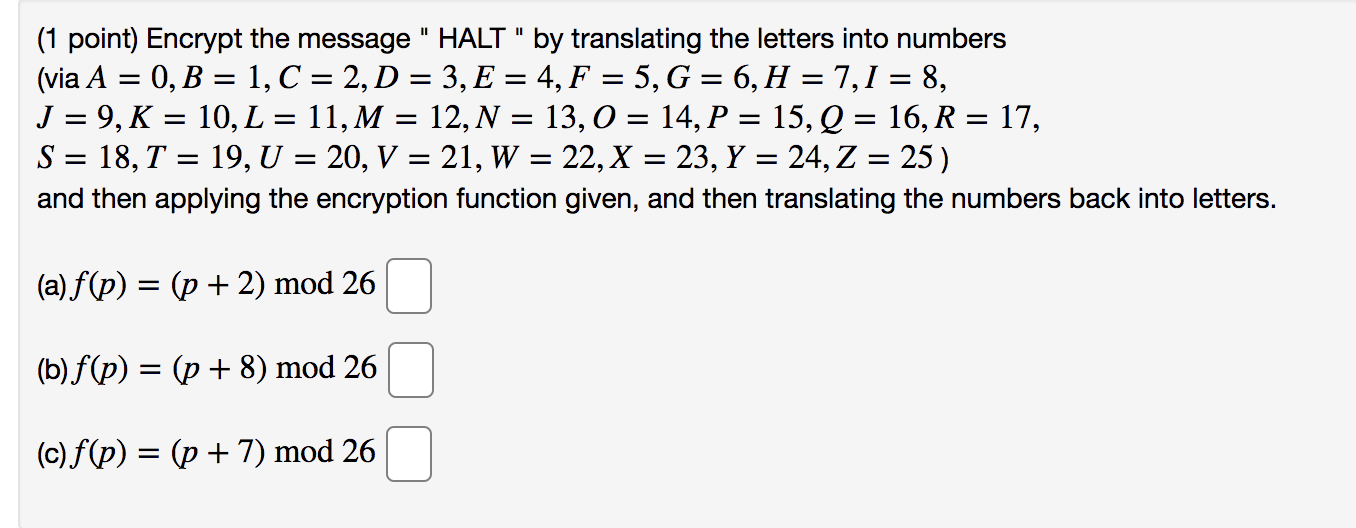
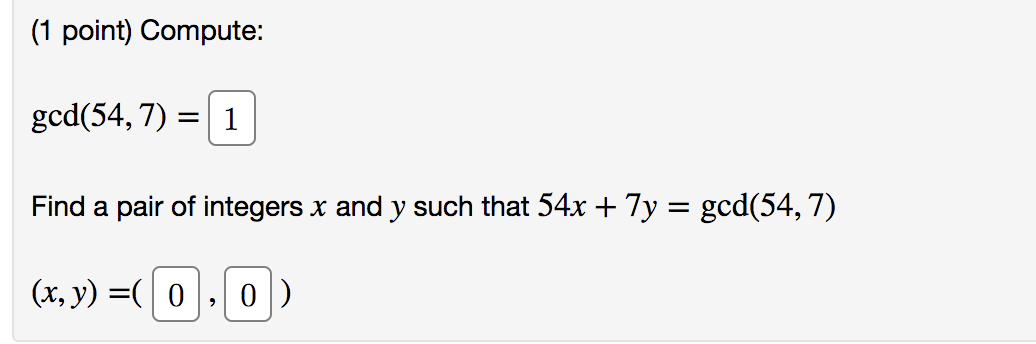
(1 point) Encrypt the message " HALT " by translating the letters into numbers (via A = 0, B = 1, C = 2, D = 3, E = 4, F = 5, G = 6, H = 7, 1 = 8, J = 9, K = 10, L = 11, M = 12, N = 13, 0 = 14, P = 15, Q = 16, R = 17, S = 18, T = 19, U = 20, V = 21, W = 22, X = 23, Y = 24, Z = 25 ) and then applying the encryption function given, and then translating the numbers back into letters. (a) f(p) = (p + 2) mod 26 (b) f(p) = (p+ 8) mod 26 (c) f(p) = (p + 7) mod 26(1 point) Compute: gcd(54, 7) = 1 Find a pair of integers x and y such that 54x + 7y = god(54, 7) (x, y) = 0 0(1 point) The goal of this exercise is to practice finding the inverse modulo m of some (relatively prime) integer n. We will find the inverse of 9 modulo 38, i.e., an integer c such that 90 E 1 (mod 38). First we perform the Euclidean algorithm on 9 and 38: 38:92: +C] C]: *4+1 [Note your answers on the second row should match the ones on the first row.] Thus gcd(9,38)=1, i.e., 9 and 38 are relatively prime. Now we run the Euclidean algorithm backwards to write 1 = 38s + 91' for suitable integers s, t. s = t = when we look at the equation 38s + 91' E 1 (mod 38), the multiple of 38 becomes zero and so we get 91' E 1 (mod 38). Hence the multiplicative inverse of 9 modulo 38 is C] (1 point) Solve the following congruence. Make sure that the number you enter is in the range [0, M 1] where M is the modulus of the congruence. 400x = 1 (mod 627) x=D ('I point) Find the smallest positive integer solution to the following system of congruence: x E 6 (mod 18) E 5 (mod 7) no