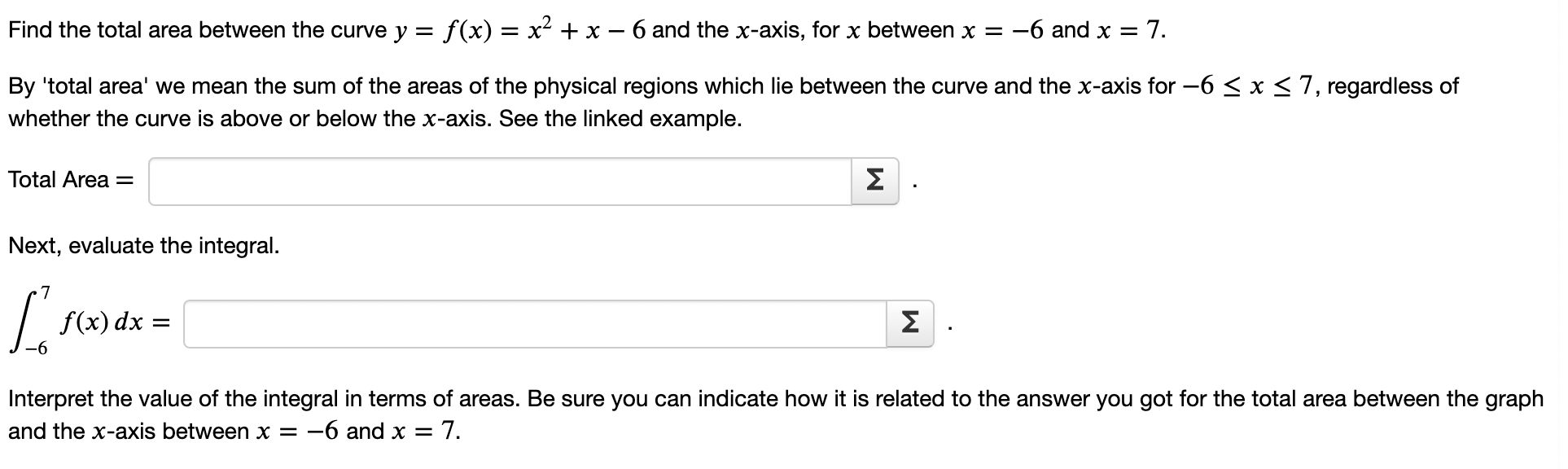
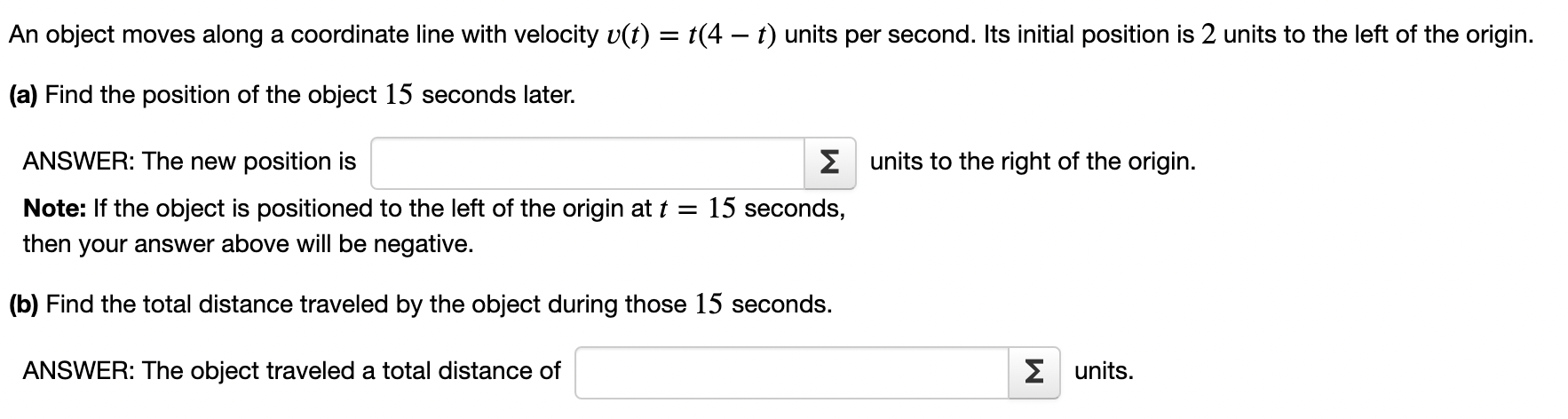
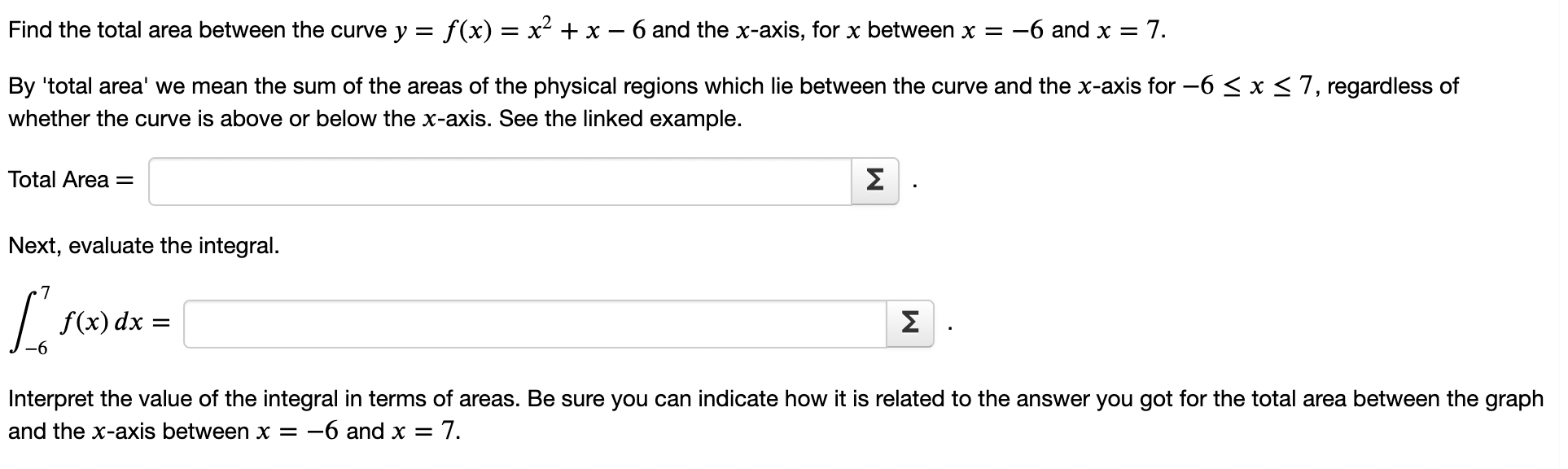
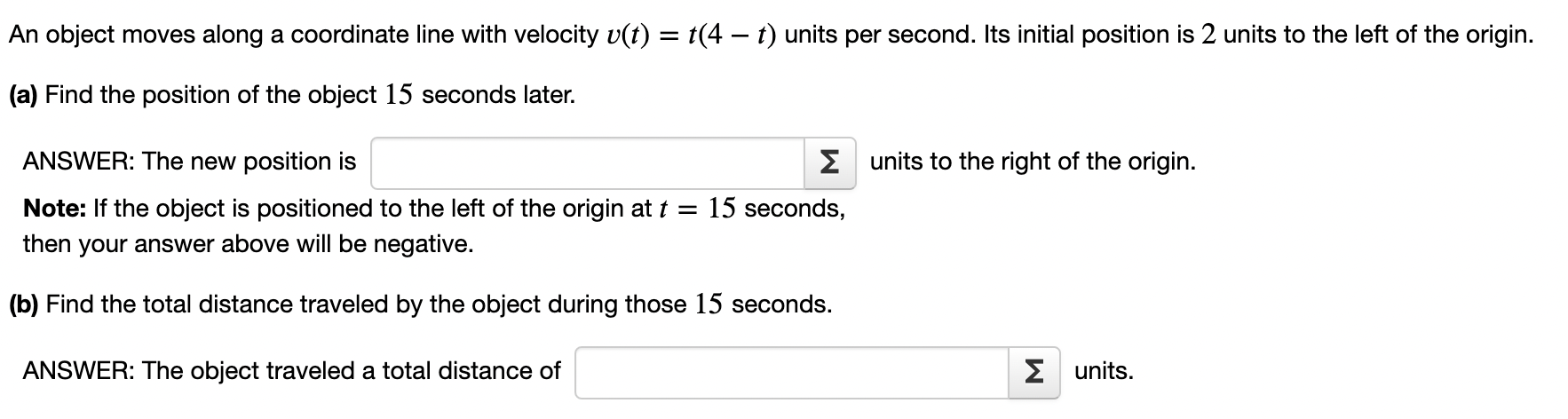
Find the total area between the curve y = f(x) = x2 + x 6 and the xaxis, for x between x = 6 and x = 7. By 'total area' we mean the sum of the areas of the physical regions which lie between the curve and the x-axis for 6 S x S '7, regardless of whether the curve is above or below the x-axis. See the linked example. Total Area = Z Next, evaluate the integral. 7 / f(x) dx = Z 6 Interpret the value of the integral in terms of areas. Be sure you can indicate how it is related to the answer you got for the total area between the graph and the xaxis between x = 6 and x = 7. An object moves along a coordinate line with velocity v(t) = 1(4 t) units per second. Its initial position is 2 units to the left of the origin. (a) Find the position of the object 15 seconds later. ANSWER: The new position is 2 units to the right of the origin. Note: If the object is positioned to the left 01 the origin at t = 15 seconds, then your answer above will be negative. (b) Find the total distance traveled by the object during those 15 seconds. ANSWER: The object traveled a total distance of 2 units. Find the average value of f(x) = 3x2 5x on the interval [2, 4]. fave = 2 From the Mean Value Theorem for Integrals, we know that there is a c in (2, 4) such that f(c) equals this average value you just found. Find c. c: 2 Find the average value of f(x) = 4x'2 on the interval [1, 5]. fave = 2 From the Mean Value Theorem for Integrals, we know that there is a c in (1, 5) such that f(c) equals this average value you just found. Find c. C: 2 Find the average value of f(x) = 5 cos x on the interval [0, 2r]. fave = 2 From the Mean Value Theorem for Integrals, we know that there is a c in (0, 12') such that f(c) equals this average value you just found. Find c. c: 2