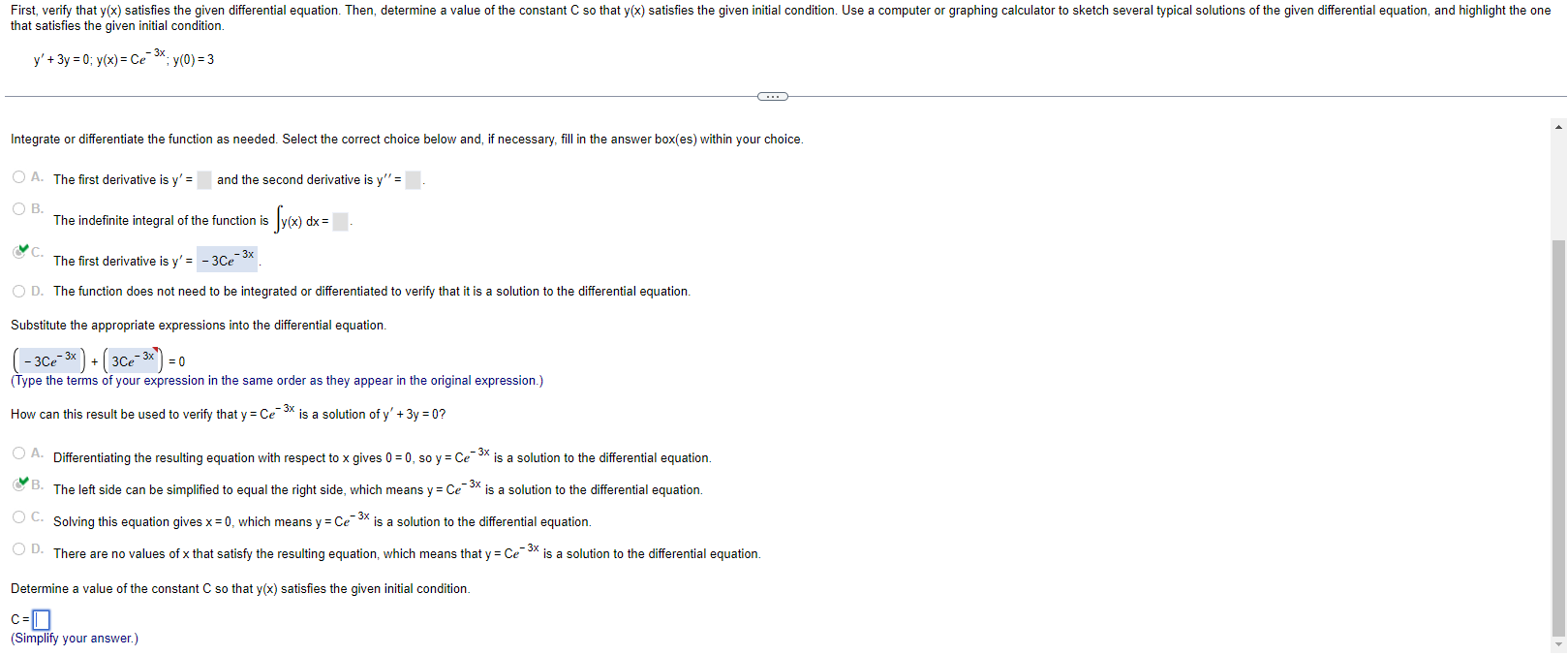
First, verify that y(x) satisfies the given differential equation. Then, determine a value of the constant C so that y(x) satisfies the given initial condition. Use a computer or graphing calculator to sketch several typical solutions of the given differential equation, and highlight the one that satisfies the given initial condition. y' + 3y = 0; y(x) = Ce->; y(0) =3 Integrate or differentiate the function as needed. Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. O A. The first derivative is y' = and the second derivative is y" = O B. The indefinite integral of the function is y(x) dx= &C. The first derivative is y' = - 3Ce- 3x O D. The function does not need to be integrated or differentiated to verify that it is a solution to the differential equation. Substitute the appropriate expressions into the differential equation. - 3Ce- 3x ) + 3Ce- 3x =0 (Type the terms of your expression in the same order as they appear in the original expression.) How can this result be used to verify that y = Ce- 3% is a solution of y' + 3y = 0? O A. Differentiating the resulting equation with respect to x gives 0 = 0, so y = Ce is a solution to the differential equation. B. The left side can be simplified to equal the right side, which means y = Ce " is a solution to the differential equation. O C. Solving this equation gives x = 0, which means y = Ce"is a solution to the differential equation. O D. There are no values of x that satisfy the resulting equation, which means that y = Ce is a solution to the differential equation. Determine a value of the constant C so that y(x) satisfies the given initial condition. C=0 (Simplify your answer.)