Fix an integer 1 and define the Markov chain (Xn)n0 on {, + 1, . . .} by the transition probabilities, pi,i+1 = 1 pi,i1 = i , i = , + 1, + 2, . . . Determine the values of for which the chain is positive recurrent, and for those values, find a stationary distribution of the chain.

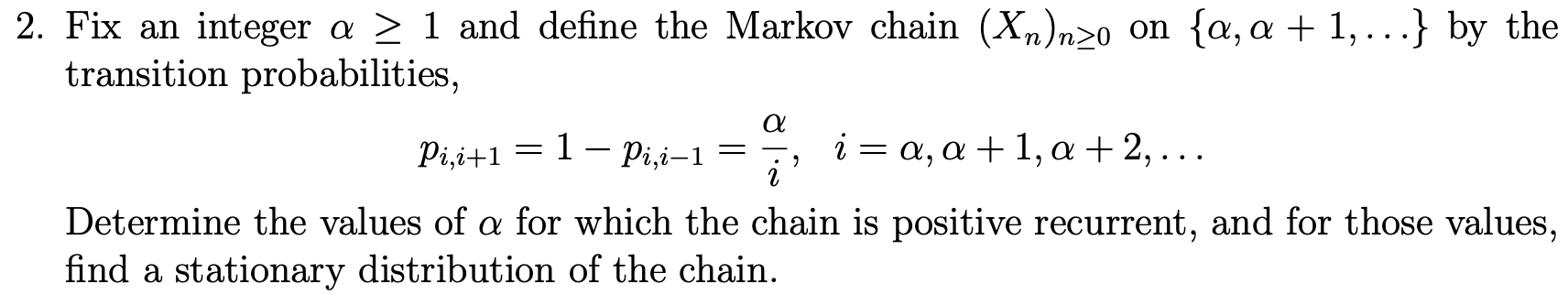
2. Fix an integer a 2 1 and define the Markov chain (Xn)no on {a, a + 1, .. .} by the transition probabilities, Pi,it1 = 1 -Pi,i-1 = i = a, a + 1, a + 2, ... Determine the values of a for which the chain is positive recurrent, and for those values, find a stationary distribution of the chain