Fix an integer 1 and define the Markov chain (Xn)n0 on {, + 1, . . .} by the transition probabilities, pi,i+1

Fix an integer α ≥ 1 and define the Markov chain (Xn)n≥0 on {α, α + 1, . . .} by the transition probabilities, pi,i+1 = 1 − pi,i−1 = α i , i = α, α + 1, α + 2, . . . Determine the values of α for which the chain is positive recurrent, and for those values, find a stationary distribution of the chain.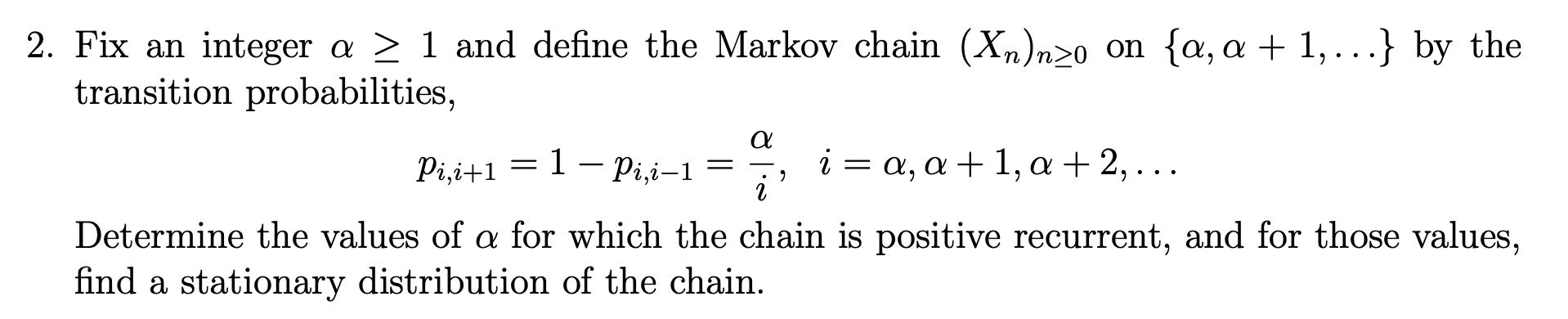

2. Fix an integer a > 1 and define the Markov chain (Xn)n>0 on {, a + 1, ...} by the transition probabilities, Pi,i+1 = 1- pi,i1 - , +1, +2, . . . Determine the values of a for which the chain is positive recurrent, and for those values, find a stationary distribution of the chain.