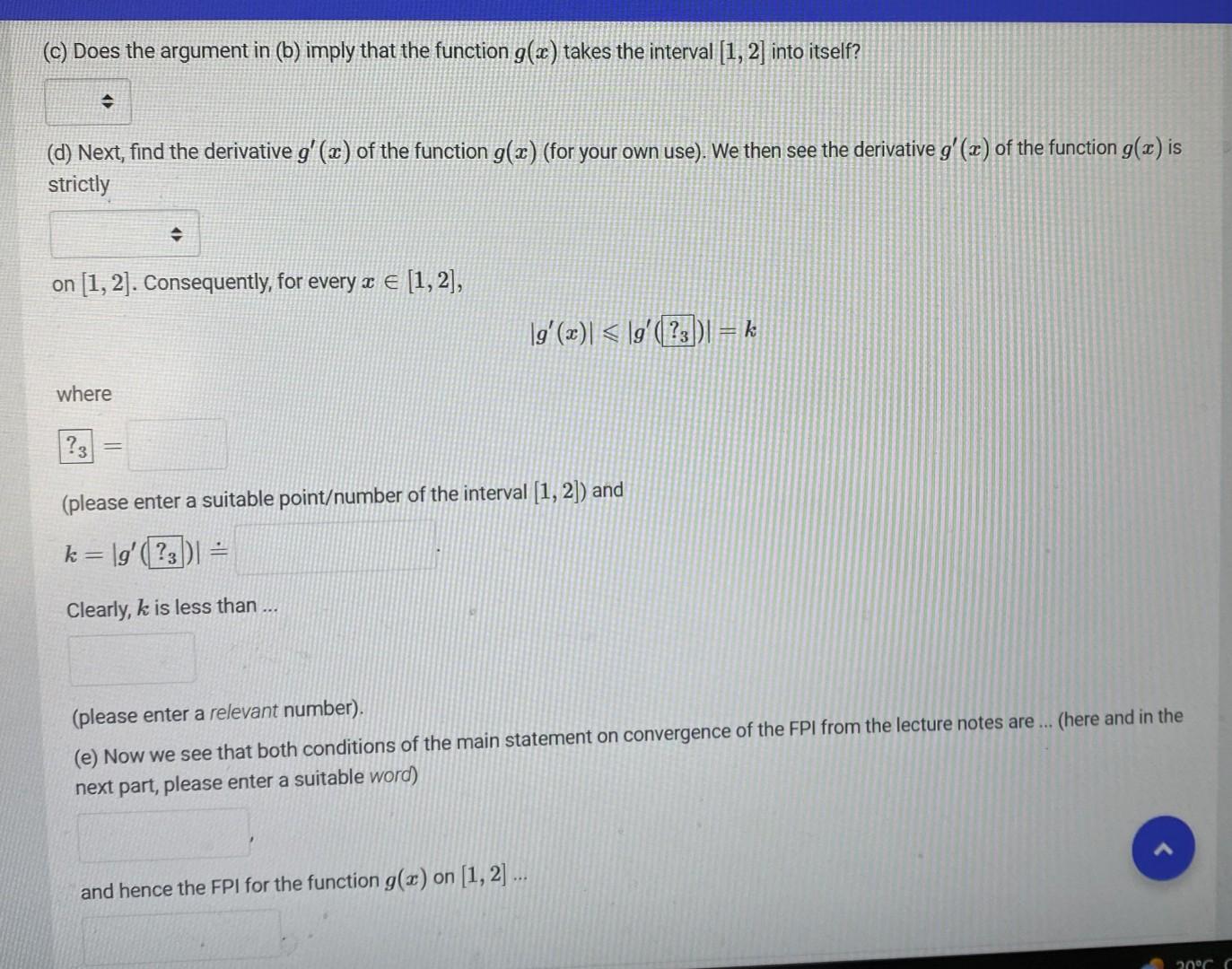
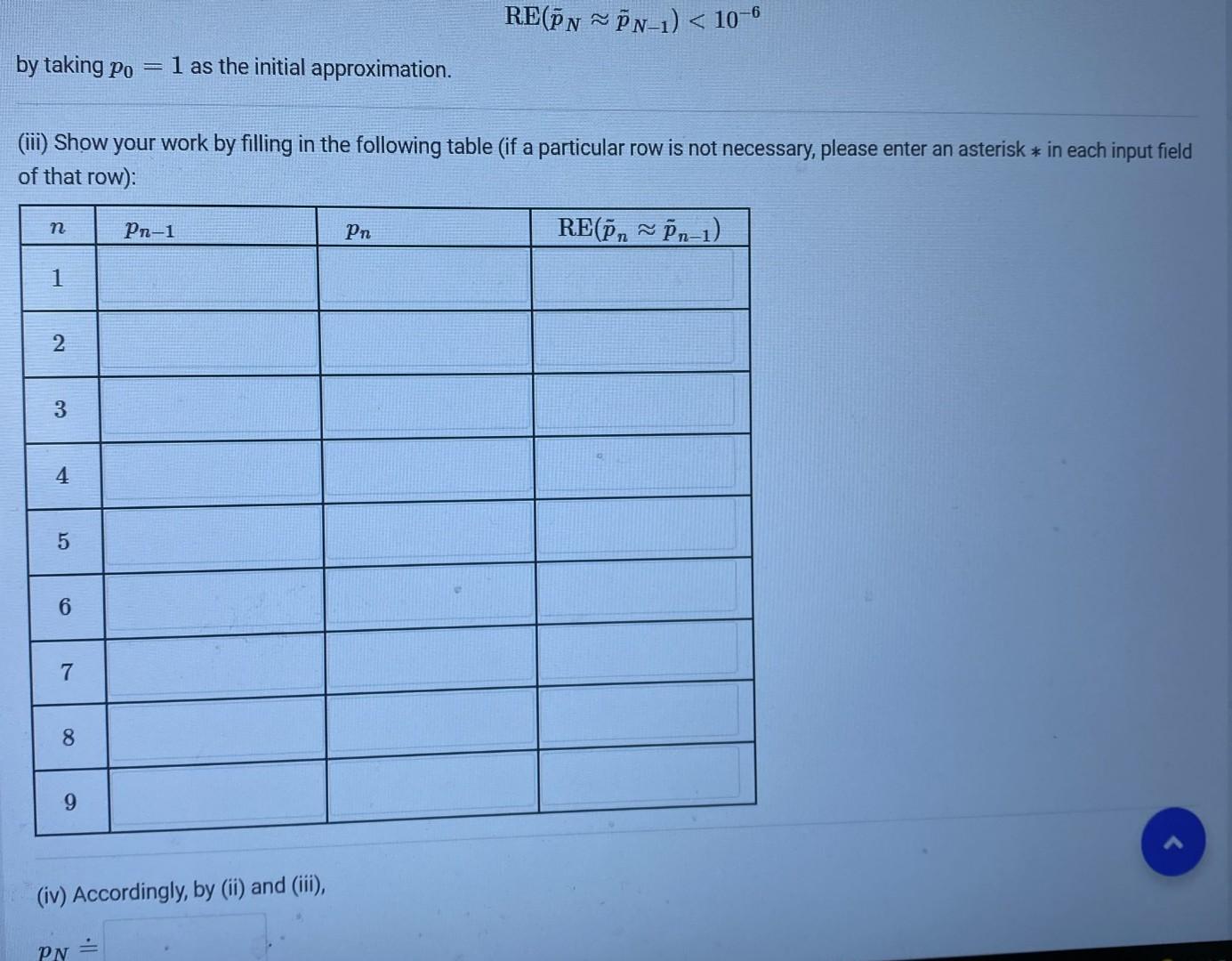
(Fixed-Point Iteration). All numerical answers should be rounded to 7 -digit floating-point numbers. Given a real number z, the symbol z~ denotes the result of rounding of z to a 7-digit floating point number. Consider the polynomial f(x)=x40.9x1.09 In what follows, we will to apply the Fixed-Point Iteration (FPI) method to approximate a unique root of the function f(x) in [1,2]. (i) (a) Show that x40.9x1.09=0x=40.9x+1.09 for all x[1,2], thereby obtaining a reduction to a fixed-point problem for the (iteration) function g(x)=40.9x+1.09 on [1,2]. (b) Clearly, the function g(x) is strictly on [1,2]. Accordingly, for every x[1,2], g(?1)g(x)g(?2) where ?1=and= (please enter suitable pointsumbers of the interval [1,2] ) and g(?1) (c) Does the argument in (b) imply that the function g(x) takes the interval [1,2] into itself? (d) Next, find the derivative g(x) of the function g(x) (for your own use). We then see the derivative g(x) of the function g(x) is strictly on [1,2]. Consequently, for every x[1,2] g(x)g(?3)=k where (please enter a suitable pointumber of the interval [1,2] ) and k=g(?3) Clearly, k is less than ... (please enter a relevant number). (e) Now we see that both conditions of the main statement on convergence of the FPI from the lecture notes are ... (here and in the next part, please enter a suitable word) RE(p~Np~N1)