Question: Flat truss to solve in pyhton E = 2 1 0 8 k N m 2 I want you to add the following explicitly step
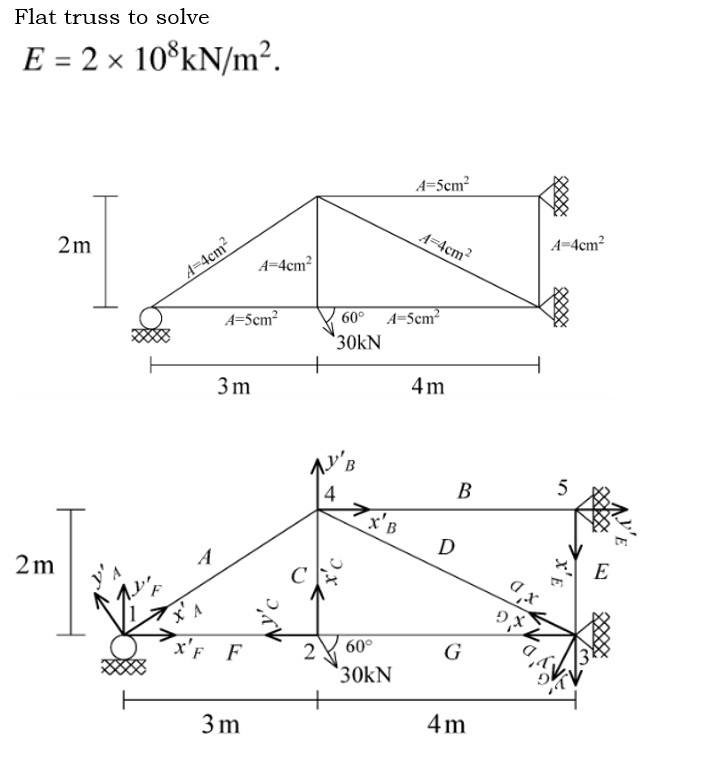
Flat truss to solve in pyhton
I want you to add the following explicitly step by step, indicating the equation that was used to solve in comments. It is to solve the exercise using the stiffness method of a truss in Python and the instructions to solve are a print on the screen the system of equations in local coordinates of each element using Python.
b print on the screen the system of equations of each element in global coordinates in python.
c Print on the screen in python the Calculation of local displacements indicating node local displacement in x is:
node local displacement in y is:
d prints on the screen the displacement in global coordinates of each bar. indicating the x global node is:
node and global is:
e Print the reactions on the screen indicating the restricted degree of freedom in python.
f Print on the screen the calculation of axial forces in each element per bar in local coordinates indicating the axial forces of bar number is:
g Print on the screen the calculation of axial forces in each element per bar in global coordinates indicating the axial forces of bar number in global x is:
axial force of bar in y global is:
h Plot the axial force of the complete structure
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
'Code to solve D trusses'
'Units are consistent and depend on the user'
# Geometry of the structure
#Input nodes and coordinates#
#Initializing node names matrix
ID
#Enter the coordinates
CoordinatesX
CoordinatesY
# Input supports
UX #####X Restriction
UY #####Y Restriction
# Input connectivity
Nodei
Nodej
# Input properties
A
E
# Input nodal loads
Fx
Fy
# Scale factor for deformations
esc
#
############################ Function definitions ###################
# Plot function
def PlotNodei Nodej ID CoordinatesX, CoordinatesY:
fig pltfigure
for i in rangelenNodei:
ni Nodeii
nf Nodeji
XX
YY
for j in rangelenID:
if ni IDj:
XXappendCoordinatesXj
YYappendCoordinatesYj
if nf IDj:
XXappendCoordinatesXj
YYappendCoordinatesYj
pltplotXX YY markero color'black'
pltshow
#
################################################################
############## Calculations begin ############################
################################################################
# Plotting the structure
PlotNodei Nodej ID CoordinatesX, CoordinatesY
# GENERATING THE GLOBAL STIFFNESS MATRIX
# Generate the global DOF Degrees of Freedom vector
nnodes lenCoordinatesX
Indices # Vector of indices ordered by DOF and ID in alphanumeric, used for assembling
for i in rangennodes:
Indices.appendx strIDi
Indices.appendy strIDi
printThe DOFs of the structure are', Indices
Indicesnum # Numeric indices vector for each DOF, used to identify rows and columns to remove
for i in rangennodes :
Indicesnum.appendi
# Identify the restricted DOFs
Restriction
for i in rangennodes:
if UXi:
Restriction.appendx strIDi
if UYi:
Restriction.appendy strIDi
printThe restricted DOFs are', Restriction
# Create the same restriction vector but in numeric form
Restrictionnum
for i in rangelenRestriction:
for j in rangennodes :
if Restrictioni Indicesj:
Restrictionnum.appendIndicesnumj
# Calculating the local and assembled matrices
# A loop is created to iterate through the number of elements,
# since local matrices are elementspecific
L # Initialize the length vector
numel lenNodei # The length of connectivity equals the number of elements
# Initialize the global stiffness matrix
K npasmatrixnpzerosnnodes nnodes
for i in rangenumel:
# Extracting coordinates
xi CoordinatesXNodeii
xj CoordinatesXNodeji
yi CoordinatesYNodeii
yj CoordinatesYNodeji
# Calculating length
Lappendxi xjyi yj
# Generating local DOF alphanumeric indices
IL
ILappendx strNodeii
ILappendy strNodeii
ILappendx strNodeji
ILappendy
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


