Follow the instructions for the Script 1, shown below:

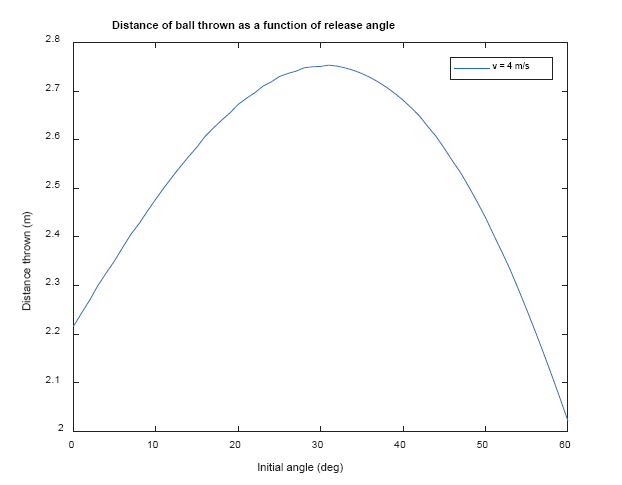
1.Turn it into a function declaration that takes v and theta as inputs and return distance, distance = DTask1_f(v, theta). The inital height is 1.5m 2. Make time go for 10 seconds and add an if statement that will display the warning 'The ball does not hit the ground in 10 seconds' If that turns out to be the case (use isempty). 3. Also, if the ball doesn't hit the ground in 10 seconds, you should return NaN as the distance. 4. To test your function, write a script DTask1.m to throw the ball with the same velocity, v=4 m/s but different angles of theta = 0:60 and plot the distance as a function of angle theta. The plot should look something like Figure 1 below. 5. You will need to run DTask1_f within a loop in order to calcculate the ditance for various thetas. 6. Change velocity to v = 60m/s, test if your program dispalys the warnings and plot the figure.

Figure 1:

Script 1:

h0 = 1.5; a = 9.8; v0 = 4; theta = 45;

t = linspace(0,1,1000);

x = v0*cos(theta*(pi/180))*t; y = h0 + v0*sin(theta*(pi/180))*t-0.5*a.*t.*t;

ind = find(y > 0 & y

fprintf ('The ball hits the ground at a disance of %f meters',htsgrndx)

figure(1) f=0; plot(x,y,[-10 10],[1 1]*f,'k--') xlim([0 3]) ylim([-1 2.5]) xlabel('Distance(m)') ylabel('Ball height(m)') title('Ball trajectory')

Distance of ball thrown as a function of release angle 2.8 v=4mis 2.7 2.6 2.5 2.4 2.3 2.2 2.1 10 20 30 40 50 80 Initial angle (deg)