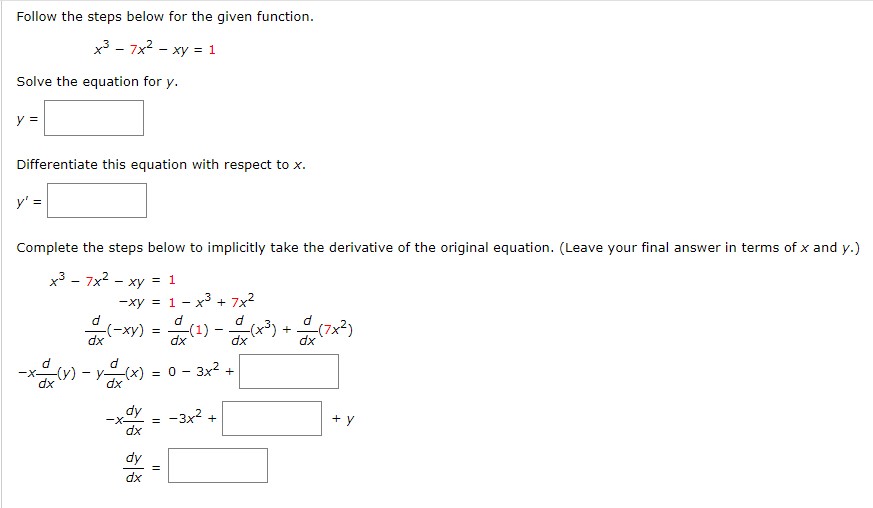
Follow the steps below for the given function. (Do not use mixed numbers in your answers.) 2x + 7y = 7 Solve the equation for y. Differentiate this equation with respect to x. y' = Complete the steps below to implicitly take the derivative of the original equation. 2x + 7y = 7 dy dx +( dy dx dy dx = 0 = = Follow the steps below for the given function. x - 7x - xy = 1 Solve the equation for y. y = Differentiate this equation with respect to x. y' = Complete the steps below to implicitly take the derivative of the original equation. (Leave your final answer in terms of x and y.) x3 - 7x - xy = 1 d -xy = 1x + 7x d dx (-xy) = d - -x(y) y(x) = 0 3x. - + dy dx dy dx = (1)-(x) + (7x) dx dx 11 -3x + +y Effect of Price on Supply of Eggs Suppose the wholesale price of a certain brand of medium-sized eggs p (in dollars/carton) is related to the weekly supply x (in thousands of cartons) by the following equation. 625p - x = 100 If 40000 cartons of eggs are available at the beginning of a certain week and the price is falling at the rate of 8c/carton/week, at what rate is the supply changing? (Round your answer to the nearest whole number.) (Hint: To find the value of p when x = 40, solve the supply equation for p when x = 40.) cartons per week Volume of a Cube The volume V of a cube with sides of length x in. is changing with respect to time. At a certain instant of time, the sides of the cube are 6 in. long and increasing at the rate of 0.3 in./s. How fast is the volume of the cube changing (in cu in/s) at that instant of time? cu in/s Watching a Helicopter Take Off At a distance of 44 ft from the pad, a man observes a helicopter taking off from a heliport. If the helicopter lifts off vertically and is rising at a speed of 51 ft/sec when it is at an altitude of 111 ft, how fast is the distance between the helicopter and the man changing at that instant? (Round your answer to one decimal place.) ft/sec