Question: For a Leftist Heap, rank(x) = 0 for a node x that is a leaf and rank(x) = 1 + min{rank(left(x)), rank(right(x))} for a node

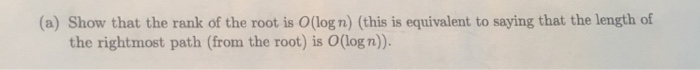
For a Leftist Heap, rank(x) = 0 for a node x that is a leaf and rank(x) = 1 + min{rank(left(x)), rank(right(x))} for a node x that is not a leaf...
Also key(x) key(x) For a Leftist Heap, rank(x) = 0 for a node x

(a) Show that the rank of the root is O(log n) (this is equivalent to saying that the length of the rightmost path (from the root) is O(log n)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Q:

Leftist Tree / Leftist Heap A leftist tree or leftist heap is a priority queue implemented with a variant of a binary heap. Every node has an s-value (or rank or distance) which is the distance to...

Q:

Skewed heaps: In this problem you are required to develop a data structure similar to that of the leftist heap. In leftist heaps, the Merge operation preserved the heap ordering and the balance...

Q:

94) A priority queue is A) is a collection that allows elements to be added, but only allows the minimum element to be removed B) a binary search tree in which the heights of the subtrees at each...

Q:

I need help with my Computer Science 2 project. I tried to post all of my program files for the project but it wouldn't let me. Develop a high-quality, menu-driven object-oriented C++ program that...

Q:

Question JAVA: Add to RedBlackBST class a method height() that computes the height of the tree (notice the height includes red and black edges and the height of a tree is the maximum depth of any...

Q:

Using the template thats given, fill in the python code while following the given guidelines in order to output a binary tree similar to the one shown. Be sure to include a function at global scale...

Q:

Give the typing rules for Peano natural numbers and their eliminator.(ii) Using the rules given above, define the addition function.] (iii) Let a binary tree be either a leaf Leaf or a node...

Q:

IN PYTHON: Please help me with this code and explain how you wrote it clearly in steps as I want to know how it works as much as possible. The goal is to make a binary tree and search it. The...

Q:

I need help with my Computer Science 2 project. I tried to post all of my codes on here but it wouldn't let me. Develop a high-quality, menu-driven object-oriented C++ program that creates a small...

Q:

In this project, we will be implementing the two rotate functions used by AVL trees, and then comparing the running time of an AVL tree vs a regular binary search tree that does not balance itself....

Q:

1. (5 points) On your Linux VM, you will find a password cracking tool called John the Ripper. Demonstrate that you are able to use this program by performing the following steps. a. (1 points) Set...

Q:

Using the SECs website (sec.gov), locate a company uses the Equity Method for its investments in securities. Does the company list the securities in its Notes? Does the company disclose the...

Q:

Multiple Choice remains constant over time. rewards investors for accepting interest rate risk. increases the real return. is inversely related to the time to maturity. compensates investors for...

Q:

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

Q:

How can Federal jobs in the same GS Pay Grade be considered jobs of Comparable Worth?

Q:

What is the Salary Range Midpoint and how does it relate to the Pay Policy Line? For which analytic is it important?

Q:

How wide are Salary Structure Ranges?