For a matrix A given below do the following.(1) Find the characteristic polynomial of A.(2) Find eigenvalues of A using the fact that at least one eigenvalue is an integer whoseabsolute value is at most 4.(3) Find eigenvectors of A. Scale them so that for each vector its coordinates do not con-tain fractions and are coprime. For example, (7,?5,10) is OK while (14,?10,20) and(7/5, ?1, 2) are not.(4) Find algebraic and geometric multiplicity of each eigenvalue.(5) Determine if A is diagonalizable. If so, find matrices P and D such that P?1AP = Dand D is a diagonal matrix. Verify this equality by computing the left-hand side. If A is not diagonalizable, prove it.Your answer must contain the characteristic polynomial and either matrices P and D or a proof that A is not diagonalizable.

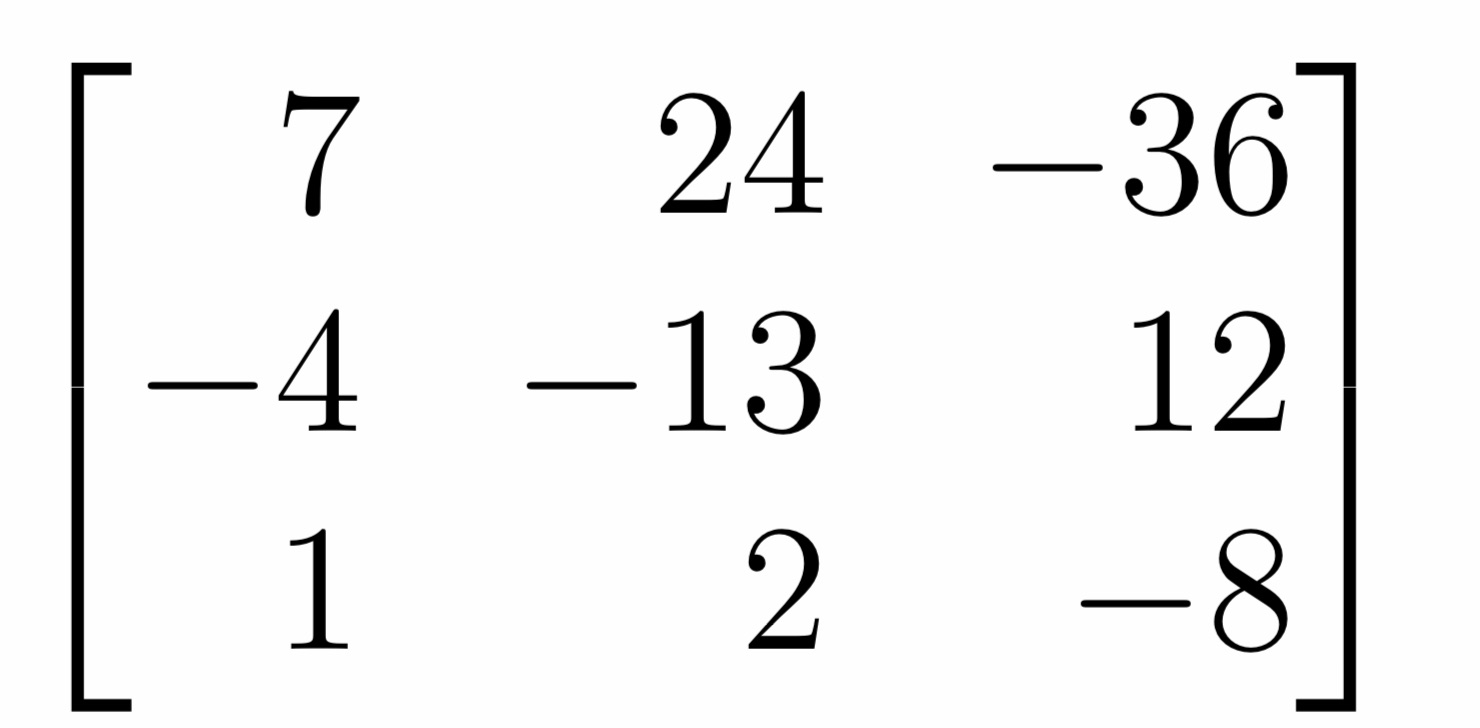
\f