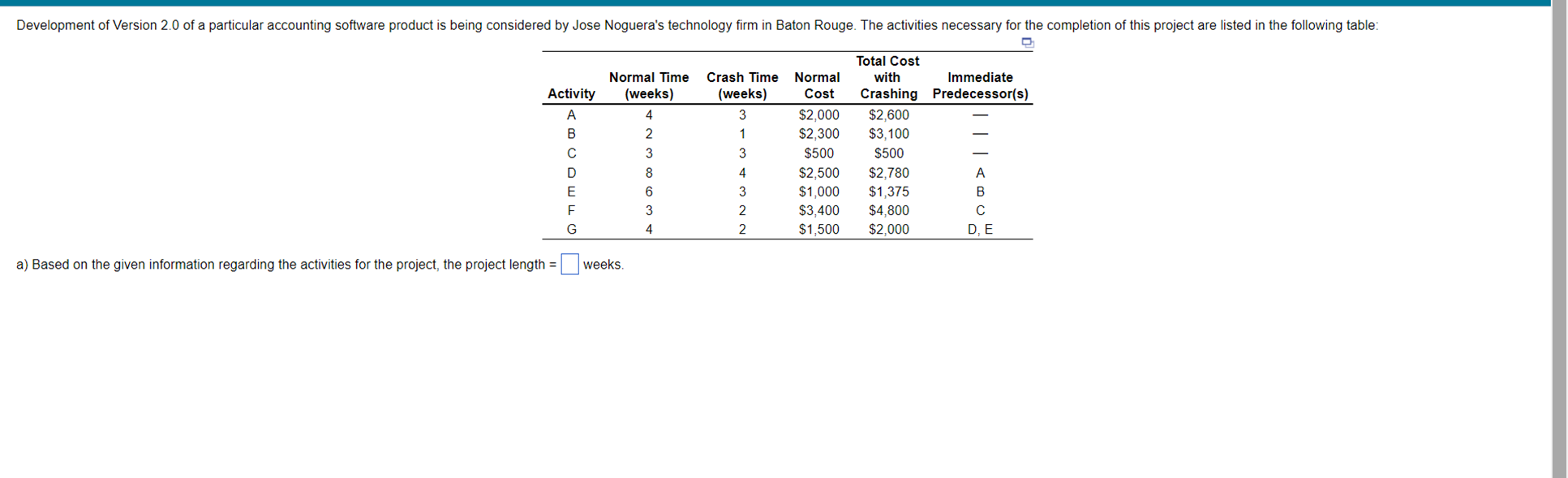
For activity D, the per week crashing cost =

= $ (Enter your response as a whole number.)

For activity G, the per week crashing cost =

= $ (Enter your response as a whole number.)

For reducing the duration of the project by one week, the activity that should be crashed first is activity:

.

The cost of the project based on the first activity selected for crashing will increase by $ (Enter your response as a whole number.)

d) What is the maximum time that can be crashed?

Path A - D - G is still critical. Of these critical activities, activity D has the lowest crash cost per week of $ . Therefore, crash activity D by 3 additional weeks to reduce the project completion time to weeks.

Note that activity D cannot be crashed any further, since it has reached its crash limit of 4 weeks.

What is(are) the critical path(s) after crashing activity D down to weeks?

Hence, any further crashing must be done to both critical paths.

Determine the crash cost per week for activities on path B - E - G.

For activity B, the per week crashing cost =

= $ (Enter your response as a whole number.)

For activity E, the per week crashing cost =

= $ (Enter your response as a whole number.)

For activity G, the per week crashing cost =

= $ (Enter your response as a whole number.)

On each of these critical paths, identify one activity that can still be crashed. Also the total cost of crashing the project should be the smallest. Note that activity

G is common to both paths. That is, by crashing this activity, we will simultaneously reduce the completion time of both paths, which yields the smallest total cost.

Therefore, crash activity G by

2 weeks. (Enter your response as a whole number.)

Activity A can still be crashed by 1 week. On path B - E - G, crash activity

E by 1 week.

Note that the project cannot be crashed any further, since all activities on path A - D - G have reached its crash limit. The maximum weeks by which the project can be reduced by crashing =

7weeks.

How much would costs increase?

Total cost of crashing the project to minimum (or maximum weeks possible) =

D's crash cost + G's crash cost + A's crash cost + E's crash cost = (Enter your response as a whole number.)

a) Based on the given information regarding the activities for the project, the project length = weeks